Предмет: Алгебра,
автор: Аноним
Исследовать числовой ряд на сходимость.
Приложения:
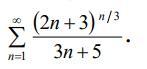
Ответы
Автор ответа:
1
Ответ:
ряд расходится
Похожие вопросы
Предмет: Окружающий мир,
автор: тоша122
Предмет: Русский язык,
автор: Никтта
Предмет: Английский язык,
автор: irisha151848
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: IntegralStarichok