Предмет: Математика,
автор: worldmen
Знайти первісну підінтегральної, функції графік якої проходить через точку з координатами (х0 ; у0)
Приложения:
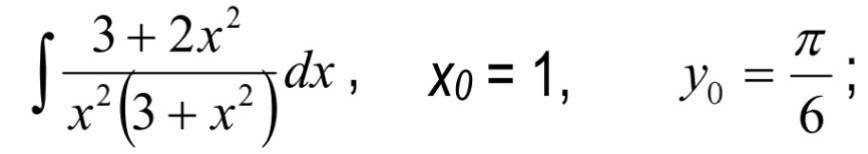
Ответы
Автор ответа:
2
Привет!)
Похожие вопросы
Предмет: Английский язык,
автор: барабере
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: Frozen2321
Предмет: Химия,
автор: shilova1810001n
Предмет: Математика,
автор: Xam163RUS