Предмет: Геометрия,
автор: valia2414
Срочно!! Помогите решить задачу!! Даю 50 балов.
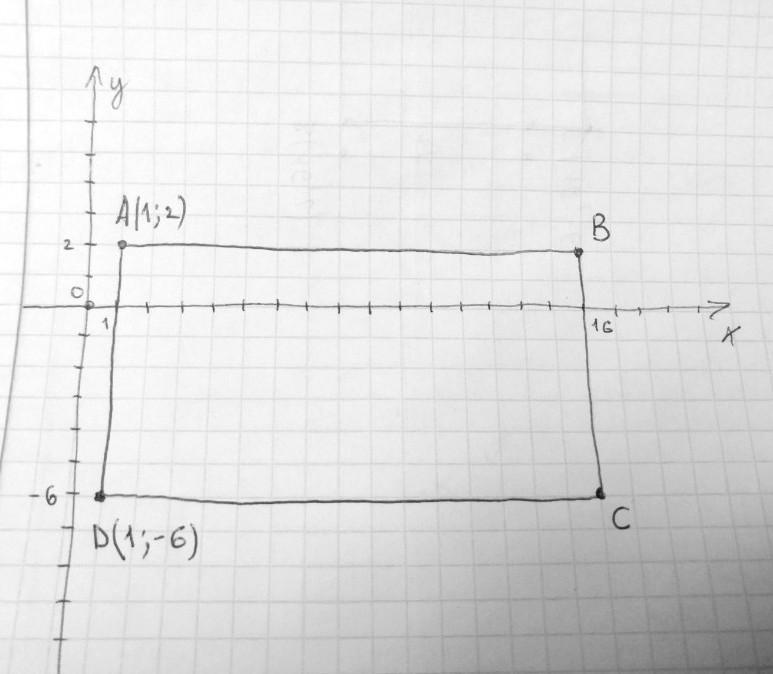
Точка А(1;2) і Д(1;-6) вершини прямокутного трикутника АБСД. Модуль вектора АС дорівнює 17. Знайдіть координати вершин Б і С.
Приложения:
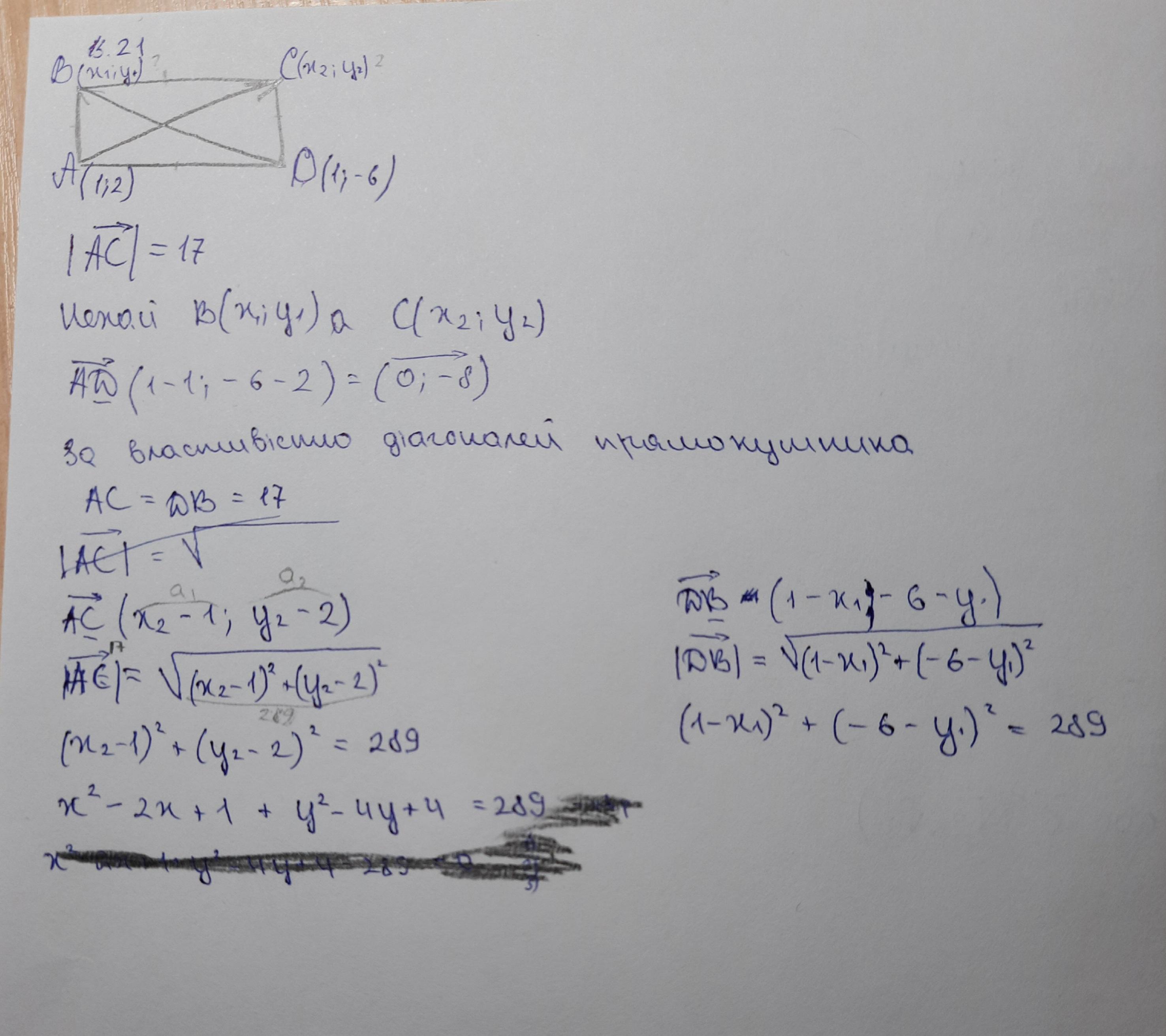
Ответы
Автор ответа:
1
Дано:
— прямоугольник
Найти:
координаты точек и
Решение:
=>
Рассмотрим треугольник — он прямоугольный. Воспользуемся Теоремой Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
=>
=>
Ответ:
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: artamon72
Предмет: Русский язык,
автор: девочка080806
Предмет: Русский язык,
автор: vikaalex69
Предмет: Английский язык,
автор: 12Мейбл2006
Предмет: Алгебра,
автор: kolyagritchin