Предмет: Алгебра,
автор: Аноним
Найти объем тетраэдра и его высоту, опущенную из вершины на грань.
Приложения:

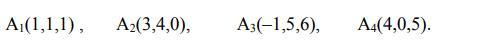
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: марго140
Предмет: Русский язык,
автор: Ранимая1
Предмет: Русский язык,
автор: arzhri
Предмет: Русский язык,
автор: artem201818
Предмет: Химия,
автор: UKALMUKO