Question

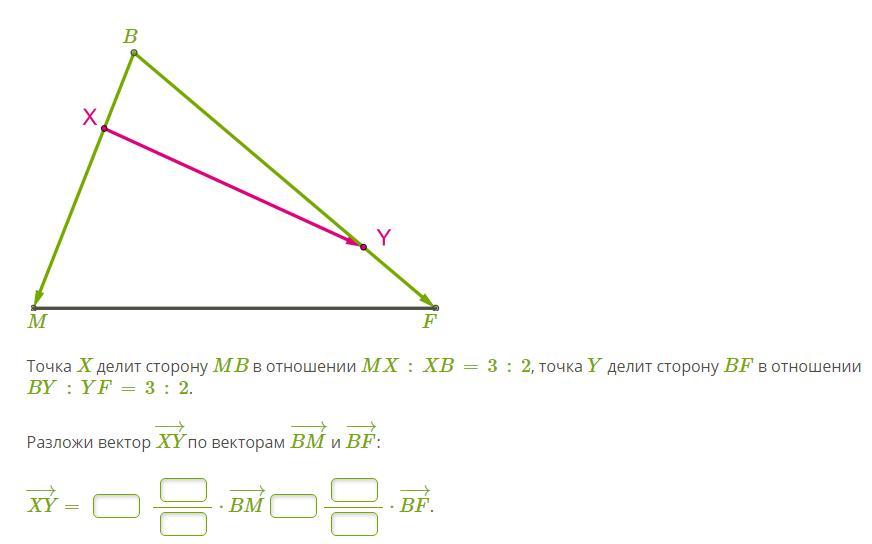
Точка X делит сторону MB в отношении MX:XB=3:2, точка Y делит сторону BF в отношении BY:YF=3:2.

Разложи вектор XY−→ по векторам BM−→− и BF−→−:

Answer 1

Ответ:

$\vec{XY} = - \frac{2}{5} \vec{BM} + \frac{3}{5} \vec{BF}$

Решение:

сложение векторов: от начальной точки вектора X до конечной точки вектора Y, "обходным путём". получается так:

$\vec{XY} = \vec{XB} + \vec{BY}$

выразим $XB$. отрезок $MB$ разделён на 5 частей (3+2=5), 2 части из из которых занимает отрезок $XB$. соответственно, $XB = \frac{2}{5} MB$

аналогично с $BY$. $BF$ тоже разделён на 5 частей (3+2=5), 3 части из которых занимает отрезок $BY$. соответственно, $BY = \frac{3}{5} BF$.

это были отрезки, их можно читать в любом направлении, но когда говорим о векторах, важно учитывать направление вектора.

вектора $\vec{BY}$ и $\vec{BF}$ имеют одно направление, поэтому знак будет "+", то есть так и оставляем, как и с отрезками: $\vec{BY} = \frac{3}{5} \vec{BF}$ .

вектора $\vec{XB}$ и $\vec{BM}$ имеют разное направление, поэтому ставим знак "–": если представить вектор $\vec{XB}$ как вектор $\vec{BX}$, который имеет одно направление с вектором $\vec{BM}$, то будет так: $\vec{BX} = \frac{2}{5} \vec{BM}$ , но $\vec{XB} = - \vec{BX}$, так как противоположно направлены, поэтому $\vec{XB} = - \frac{2}{5} \vec{BM}$.

получается,

$\vec{XY} = \vec{XB} + \vec{BY} = - \frac{2}{5} \vec{BM} + \frac{3}{5} \vec{BF}$