Предмет: Алгебра,
автор: vladgasimov2000
При каких значениях переменной имеет смысл выражение
Приложения:
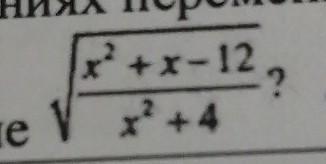
Ответы
Автор ответа:
0
Значения переменной, при которых выражение имеет смысл это область допустимых значений (ОДЗ).
Мы знаем, что выражение под квадратным корнем не может быть отрицательным, а знаменатель не должен быть равным нулю, т.к. на 0 делить нельзя. Поэтому составим систему неравенств:
Чтобы решить систему неравенств, нужно решить каждое неравенство и найти их объединение. В первом дробно-рациональном неравенстве получаем:
Во втором получаем:
Значит, ответом будут являться все значения x в этом интервале:
Похожие вопросы
Предмет: Окружающий мир,
автор: зайка275
Предмет: Українська мова,
автор: Мамкумал
Предмет: Окружающий мир,
автор: Fuio
Предмет: Русский язык,
автор: alexaverin61
Предмет: Алгебра,
автор: maksimzvazhy