Предмет: Геометрия,
автор: starmini747
Сторона квадрата ABCD равна 8 см. Точка S находится на расстоянии
16 см от его вершин. Найти расстояние от точки S до плоскости квадрата.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
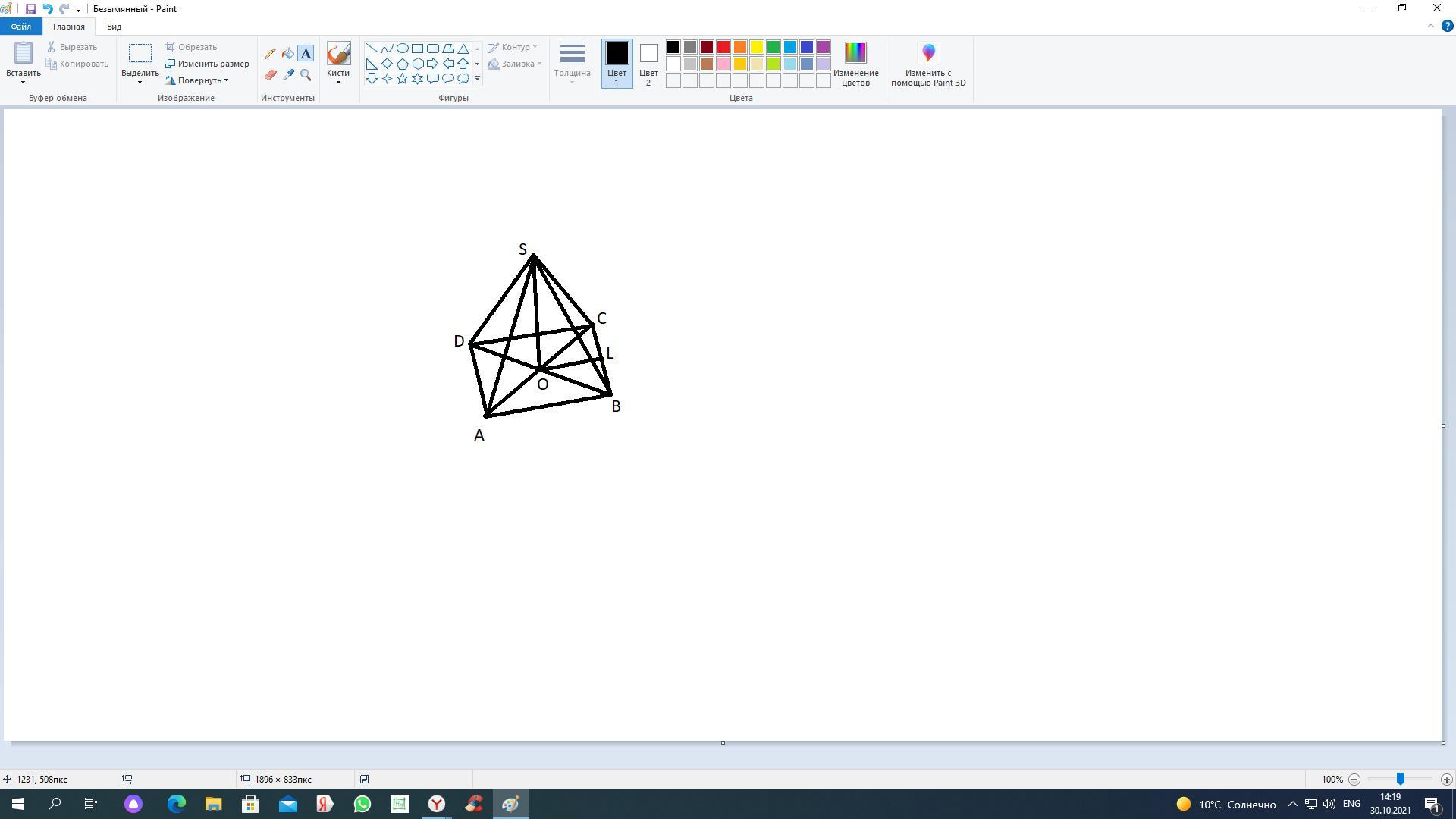
фигура будет пирамидой с основанием квадрата
точка s равноудаленна от всех вершин, а это значит она падает на пересечение диагоналей как высота, эта и высота и есть расстояние которое надо найти
ABCD квадрат
проведем диагонали
в треугольнике ACB, OL средняя линия = 4 (половина АВ)
в треугольнике СОВ, OL медиана биссектриса высота
BL=LC=4
SB=SA=SD=SC=16
SL=как катет прям треугольника =
OS как катет прям треугольника (так как она высота) = см
на рисунке нету только углов ( обозначение ) и прямой SL
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: СоняУхмыленко
Предмет: Окружающий мир,
автор: daniildavydov2006
Предмет: Английский язык,
автор: asdfg12647
Предмет: История,
автор: ivanbulban
Предмет: Французский язык,
автор: MuratBoz2004