Предмет: Алгебра,
автор: keksik708
Найдите пожалуйста сумму ряда
Приложения:
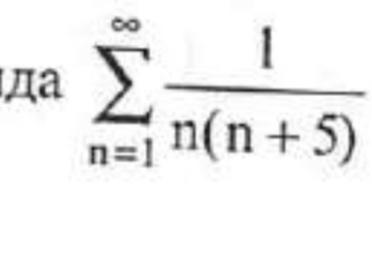
Аноним:
137/300
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: vera197
Предмет: Окружающий мир,
автор: lba8080
Предмет: Немецкий язык,
автор: MrTvister111
Предмет: Математика,
автор: Аноним