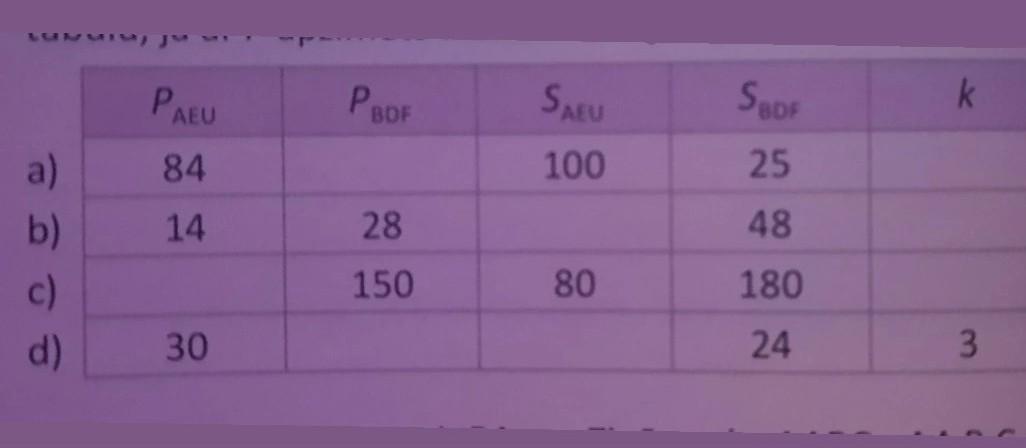
Известно, что AEU и BDF подобны и имеют коэффициент подобия k. Заполните таблицу, если P обозначает периметр соответствующего треугольника, а S-площадь.
Ответы
Ответ:
a) 84-42-100-25-2
b) 14-28-12-48-0.5
c) 100-150-80-180-2/3
d) 30-10-216-24-3
Объяснение:
AE=k*BD, EU=k*DF, AU=k*BF
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
100/25=4=2², т.е. коэффициент подобия равен двум, значит, стороны первого треугольника в два раза больше сторон второго треугольника, тогда периметр первого треугольника в два раза больше периметра второго треугольника: 84/2=42
Сторона первого треугольника в два раза меньше стороны второго треугольника, значит, площадь первого треугольника в 4 раза меньше площади второго треугольника.
14/28=0,5; 0,5²=0,25; 0,25*48=12
Площадь первого треугольника относится к площади второго треугольника как 80/180=4/9. Значит, коэффициент подобия равен корню из этого значения √4/9=2/3. Т.е. периметр первого треугольника составляет 2/3 периметра второго треугольника: 2/3*150=100
Коэффициент подобия равен 3, значит, стороны первого треугольника в три раза больше сторон второго треугольника. Значит, периметр первого в три раза больше периметра второго, а площадь первого в 3²=9 раз больше площади второго треугольника.
30/3=10; 24*9=216