Предмет: Геометрия,
автор: alidjdnevaminara721
ради бога помогите пожалуйста!!
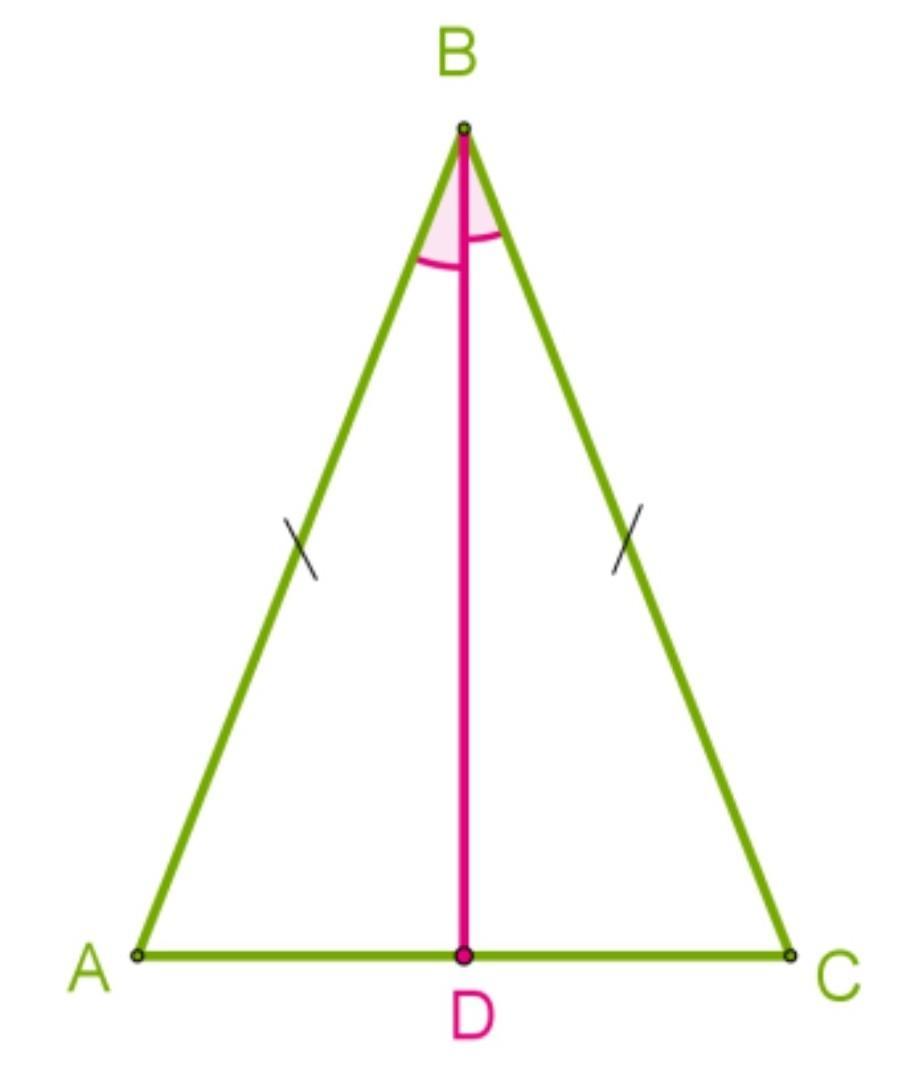
В равнобедренном треугольнике с длиной основания 23 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.

Рассмотрим треугольники ΔABD и Δ (треугольник записать в алфавитном порядке);
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ ;
2. так как проведена биссектриса, то ∡ = ∡ CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — .
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
AD= см.
Приложения:
alidjdnevaminara721:
просто их там много
ещё раз спасибо что помогаешь^^
а почему ты не отвечаешь а пишешь комментарии? можно же заработать баллы
Рассмотрим треугольники АВД и ∆ВСД. Остальное по порядку.
спасибо^^
1) С
2) АВД
3) равнобедренный.
2) АВД
3) равнобедренный.
АД=11,5
спасибо^^
ааа, спасибо тебе я 5 получила
я бесконечно тебе благодарна!!!!
Ответы
Автор ответа:
0
Рассмотрим треугольник ABC(равнобедренный по усл.)
AB=BC(по усл.) =>
AD=DC(т.к. в равноб. треугол. BD-биссектриса, медиана, высота)
AD=DC=ADC:2=23:2=11,5см
У треугольников ABD, CBD-BD является общей стороной=>
Треугольник ABD=треугольнику BDC
по 2 признаку(УСУ)
AB=BC(по усл.) =>
AD=DC(т.к. в равноб. треугол. BD-биссектриса, медиана, высота)
AD=DC=ADC:2=23:2=11,5см
У треугольников ABD, CBD-BD является общей стороной=>
Треугольник ABD=треугольнику BDC
по 2 признаку(УСУ)
Похожие вопросы
Предмет: Русский язык,
автор: валерия21213
Предмет: Английский язык,
автор: Imychka
Предмет: Русский язык,
автор: LANA081073
Предмет: Русский язык,
автор: marishatrova