Предмет: Алгебра,
автор: Ифигения
Найти dy/dx
e^(x-y) = x/y
Приложения:
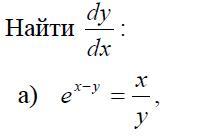
Ответы
Автор ответа:
1
Ответ:
Ифигения:
Большое спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: ash2pac2
Предмет: Окружающий мир,
автор: влада2031
Предмет: Русский язык,
автор: Валерия0410
Предмет: Алгебра,
автор: qwerty3579
Предмет: Алгебра,
автор: culickowaanast