Question

помогите пожалуйста умоляю напишите пожалуйста дано и решение и т.д. 1 и 2 задание и если поместиться 3​

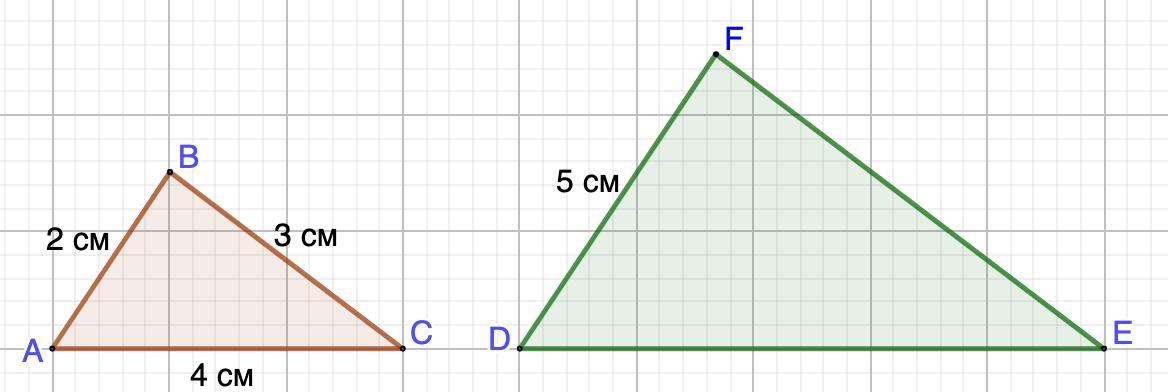
Стороны треугольника равны 2см,3см, 4 см найдите стороны подобного ему треугольника если Его меньшая сторона 5 см

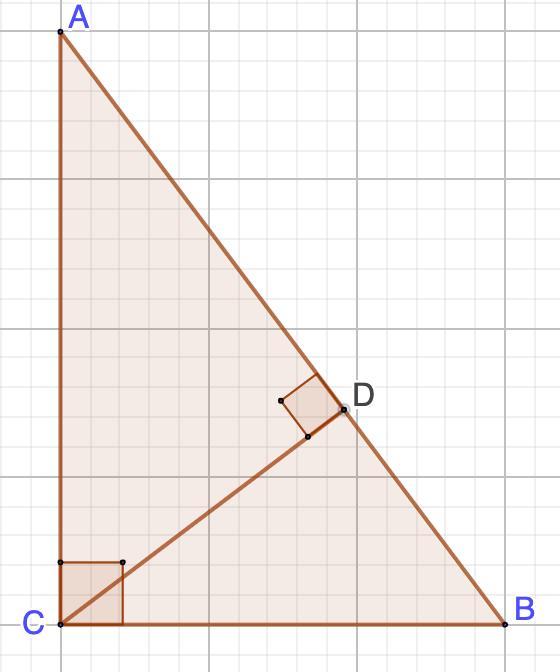
В прямоугольном треугольнике АВС (LC- прямой)Проведена высота CD. Докажите, что треугольники ACD подобен треугольнику АВС

Answer 1

Объяснение:

1. Дано: ΔАВС ~ ΔDFE

AB=2 см; BC=3 см; AC=4 см.

DF=5 см.

Найти: DE; FE.

Решение:

• Подобные треугольники это треугольники, у которых углы равны, а соответствующие стороны пропорциональны.

Составим пропорцию и найдем нужные стороны:

$\displaystyle \frac{AB}{DF}=\frac{BC}{FE}=\frac{AC}{DE}$

Подставим значения:

$\displaystyle \frac{2}{5}=\frac{3}{FE}\\\\FE=\frac{5*3}{2} }= \frac{15}{2}=7,5 \;(_{CM})$

$\displaystyle \frac{2}{5}=\frac{4}{DE} \\\\DE=\frac{5*4}{2}=10\;(_{CM)}$

EF=7,5 см; DE=10 см.

2.

Дано: ΔАВС - прямоугольный.

CD - высота.

Доказать: ΔACD~ΔABC.

Доказательство:

Рассмотрим ΔACD и ΔABC - прямоугольные.

∠С=∠CDA=90°

∠A - общий.

• Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

⇒ ΔACD~ΔABC (1-й признак подобия треугольников.