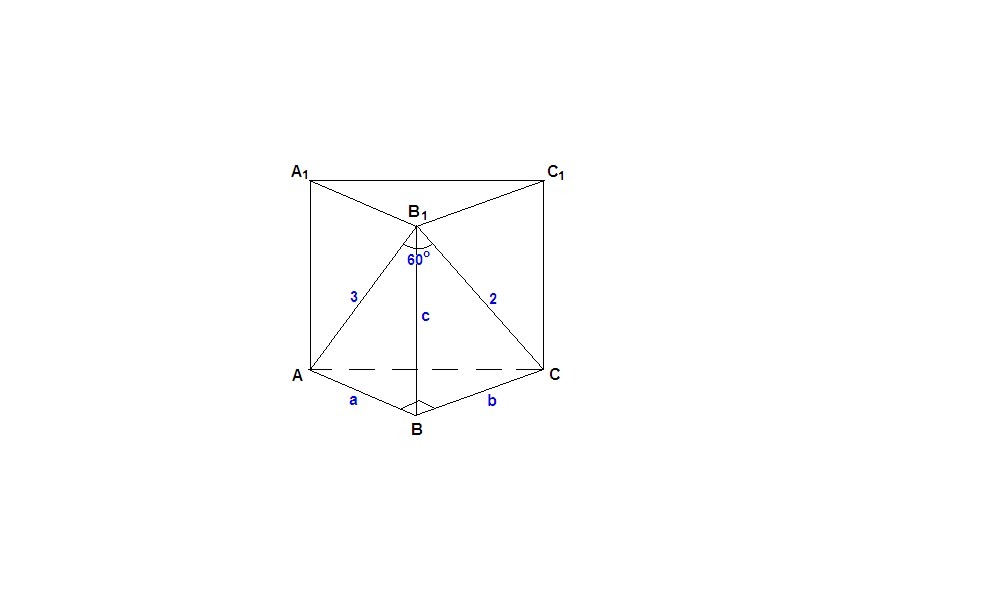
найдите объем прямой призмы abca1b1c1 если угол ab1c=60 градусов ab1=3, cb1=2
Ответы
Условие задачи неполное. Должно быть так:
Найдите объем прямой призмы АВСАВ₁С₁, если
∠АВ₁С = 60°, АВ₁ = 3, СВ₁ = 2 и двугранный угол с ребром ВВ₁ прямой.
Призма прямая, значит боковые грани - прямоугольники. Тогда
АВ⊥ВВ₁, СВ⊥ВВ₁, значит ∠АВС = 90° - линейный угол двугранного угла с ребром ВВ₁.
Из треугольника АВ₁С по теореме косинусов найдем АС:
АС² = AB₁² + CB₁² - 2·AB₁·CB₁·cos∠AB₁C
AC² = 9 + 4 - 2 · 3 · 2 · 1/2 = 13 - 6 = 7
AC = √7
Пусть АВ = а, ВС = b, ВВ₁ = с.
По теореме Пифагора составим три уравнения:
ΔАВС: a² + b² = 7
ΔABB₁: a² + c² = 9
ΔCBB₁: b² + c² = 4
Получили систему из трех уравнений с тремя переменными. Сложим все три уравнения:
2(a² + b² + c²) = 20
a² + b² + c² = 10
Теперь из этого уравнения вычтем каждое. Получим:
с² = 3
b² = 1
a² = 6
Откуда:
с = √3, b = 1, a = √6.
V = Sabc · BB₁ = 1/2 · ab · c = 1/2 · √6 · 1 · √3 = 3√2/2