Question

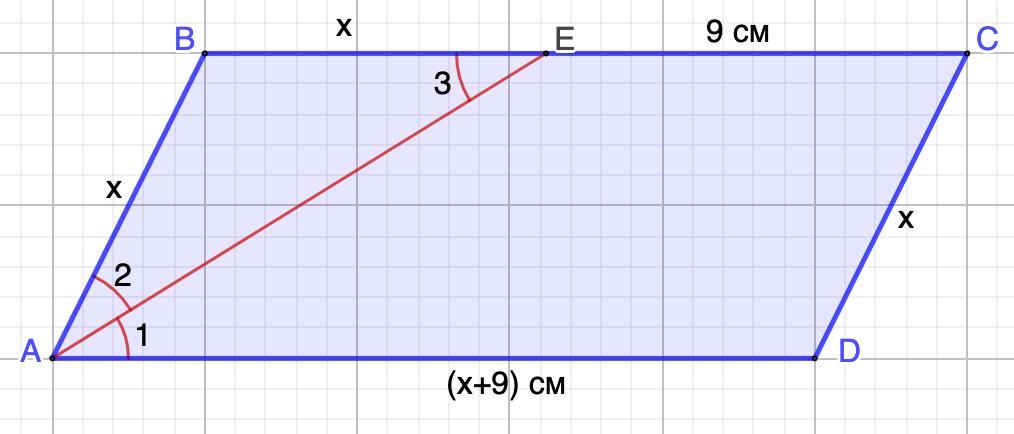
В параллелограме ABCD проведена биссектриса AE, причем EC=9см. Найдите стороны AB и BC, если периметр равен 54. а AB - меньшая сторона. СРОЧНО ДАЮ 40 БАЛЛОВ!!!!

Answer 1

Ответ:

АВ =  9 см

ВС = 18 см

Объяснение:

Дано: ABCD - параллелограмм;

АЕ - биссектриса;

ЕС = 9 см; Р (АВСD) = 54 см.

Найти: АВ; ВС.

Решение:

Рассмотрим ΔАВЕ.

∠1 = ∠2 (АЕ - биссектриса)

∠1 = ∠3 (накрест лежащие при BC || AD и секущей АЕ)

⇒ ∠2 = ∠3

⇒ Δ АВЕ - равнобедренный (углы при основании равны)

Пусть АВ = ВЕ = х (см), тогда ВС = (х+9) см.

• Противоположные сторона параллелограмма равны.

⇒ АВ = СD =х см; ВС = AD = (х+9) см

• Периметр параллелограмма равен удвоенной сумме смежных сторон.

Р (ABCD) = 2(х+х+9)

54=4х+18

4х=36

х=9

⇒ АВ = СD =х = 9 см

ВС = AD = (х+9) = 18 см