Question

25 БАЛОВ! Написати рівняння прямої 2x – y + 1 = 0, що проходить через точку М(-1;2) перпендикулярно до заданої прямої і знайти їх точку перетину;

Answer 1

Будем считать, что задание дано так:

Написати рівняння прямої , що проходить через точку М(-1;2) перпендикулярно до заданої прямої  2x – y + 1 = 0 і знайти  точку їх перетину.

Заданная прямая дана в общем виде Ах + Ву + С = 0.

У перпендикулярной прямой коэффициенты А и В меняются на -В и А.

Получаем х + 2у + С = 0.

Для определения слагаемого С подставим координаты точки М(-1; 2), через которую проходит перпендикулярная прямая.

-1 + 2*2 + С  = 0, С = 1 - 4 = -3.

Уравнение перпендикуляра через точку М: х + 2у - 3 = 0.

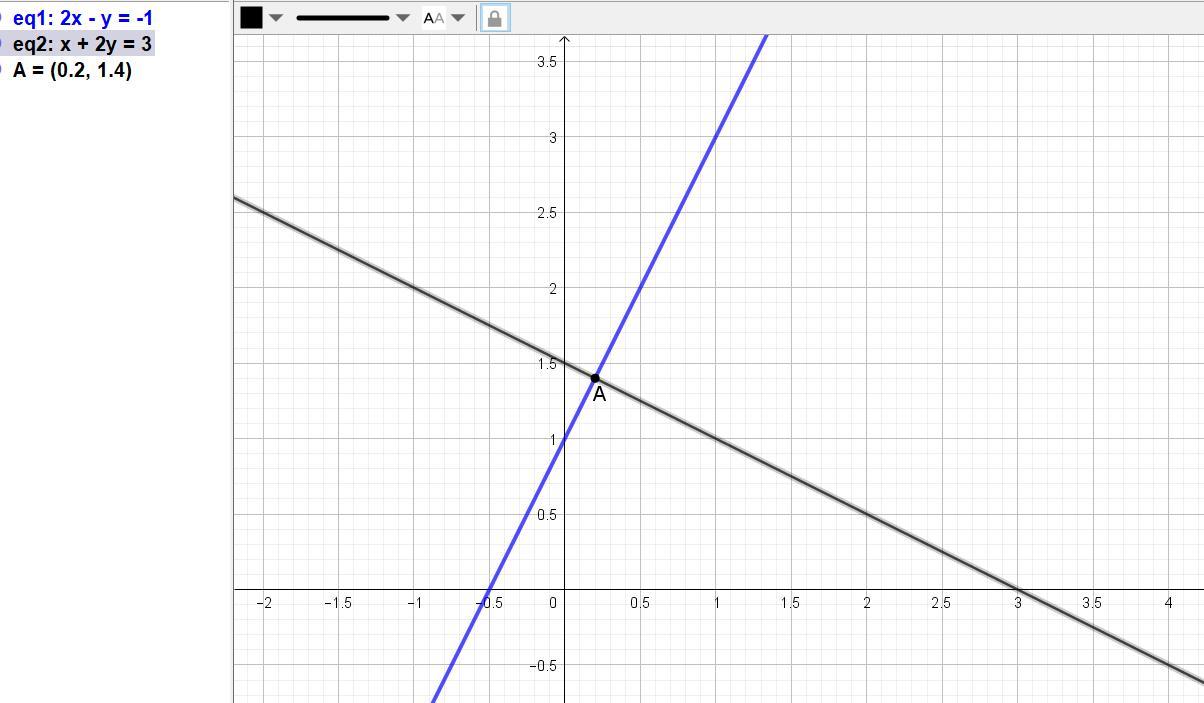
Для определения точки пересечения прямых надо решить систему:

{2x – y + 1 = 0 |x(2) =  4x - 2y + 2 = 0

{х + 2у - 3= 0               х + 2у - 3 = 0  

                                    5x        - 1 = 0.

x = 1/5 = 0,2, y = 2x + 1 = 2*(1/5) + 1 = 7/5 = 1,4.