Предмет: Алгебра,
автор: thealdik
Даю 50 баллов. Решите пожалуйста срочно
Приложения:
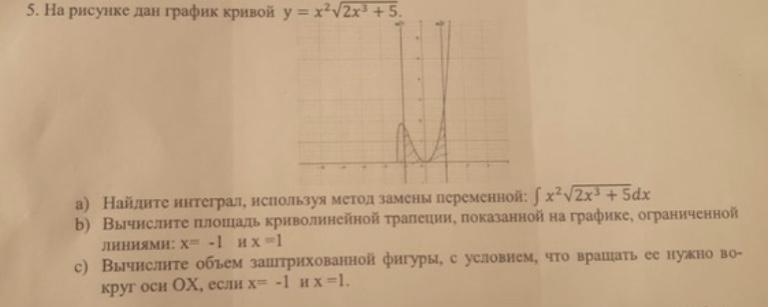
Ответы
Автор ответа:
1
Ответ:
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: Арука221
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: 55555t
Предмет: Математика,
автор: nikulinasanya