Question

Срочно! 100 БАЛЛОВ!
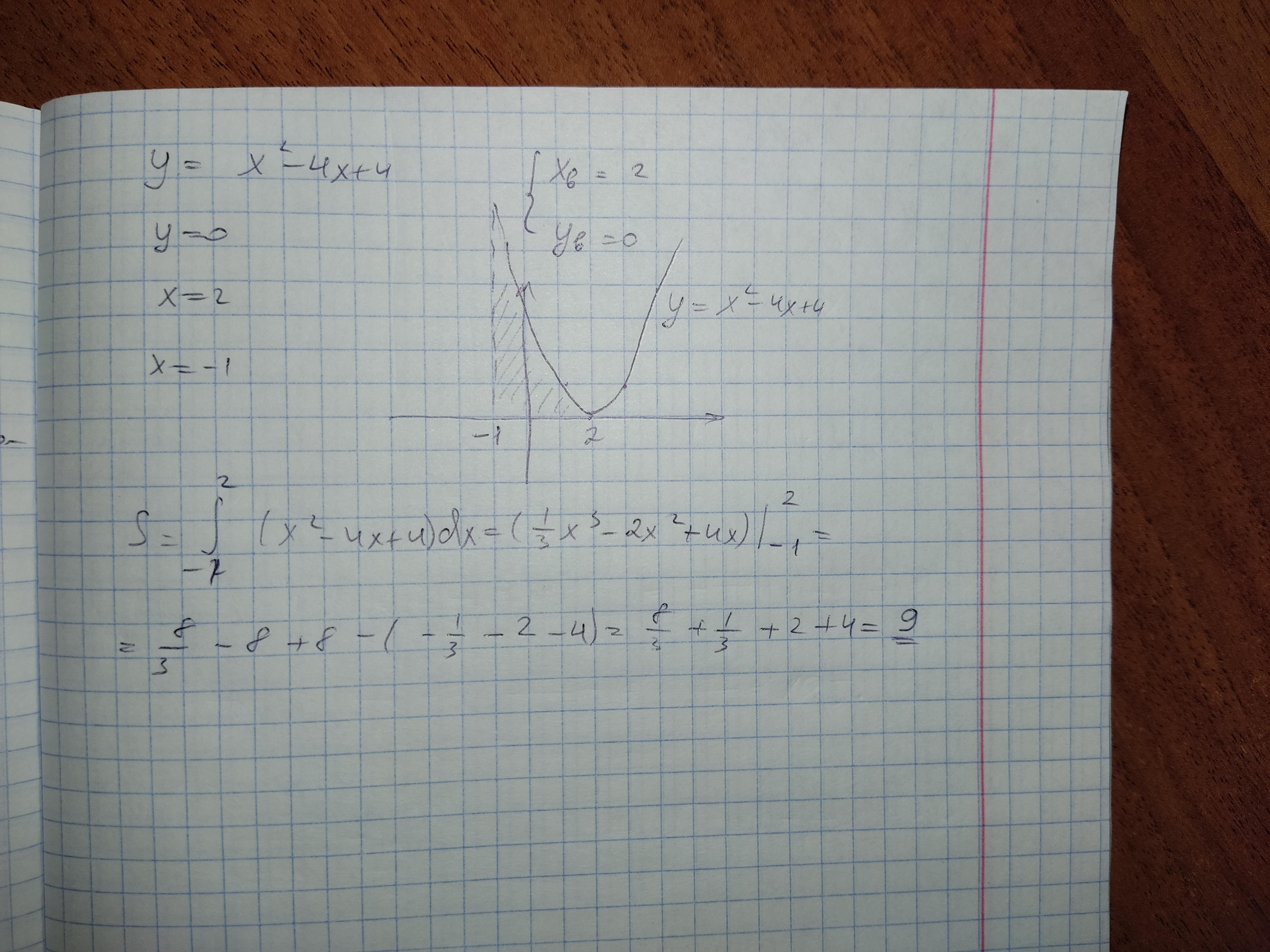
Вычислите площадь фигуры, ограниченной линиями: у=х²-4х+4, у=0,х=2, х=-1
Критерии:
изображает на координатной плоскости область, ограниченную линиями
составляет уравнение, находит пределы интегрирования
применяет формулу Ньютона – Лейбница
вычисляет площадь искомой фигуры;

Answer 1

Объяснение:

$y=x^2-4x+4\ \ \ \ y=0\ \ \ \ x=2\ \ \ \ x=-1\ \ \ \ S=?\\S=\int\limits^2_{-1} {(x^2-4x+4-0)} \, dx=\int\limits^2_{-1} {(x^2-4x+4)} \, dx =\int\limits^2_{-1} {(x-2)^2} \, dx.\\\int\limits {(x-2)^2} \, dx.\\x-2=u\ \ \ \ dx=du\ \ \ \ \Rightarrow\\\int\limits {u^2} \, du=\frac{u^3}{3}.\\\frac{(x-2)^3}{3}\ |_{-1}^2=\frac{(2-2)^3}{3}-\frac{(-1-2)^3}{3} =\frac{0^3}{3}-\frac{(-3)^3}{3}=0-(-\frac{27}{3})=-(-9)=9.$

Ответ: S=9 кв. ед.

Answer 2

Ответ:

Объяснение:

На фото записал решение по нужным критериям