Предмет: Математика,
автор: sallupgazmanov
Помогите пожалуйста
Приложения:
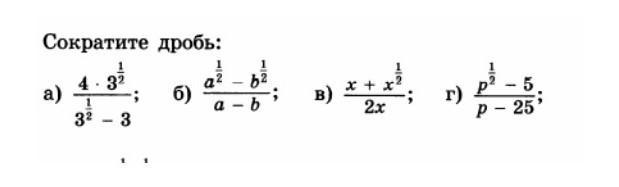
Ответы
Автор ответа:
0
Пошаговое объяснение:
а) В знаменателе вынесем общий множитель и сократим дробь:
б) Разложим знаменатель на множители, используем формулу разности квадратов
a²-b²=(a-b)(a+b)
в) Вынесем в числителе общий множитель, в знаменателе представим х в виде степени с показателем 2:
г) Разложим знаменатель на множители, используем формулу разности квадратов
a²-b²=(a-b)(a+b)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: sonyalol56
Предмет: Химия,
автор: orionillarion
Предмет: Алгебра,
автор: vladimir7481