Предмет: Геометрия,
автор: dz356211
Помогите пж не могу сделать
Приложения:
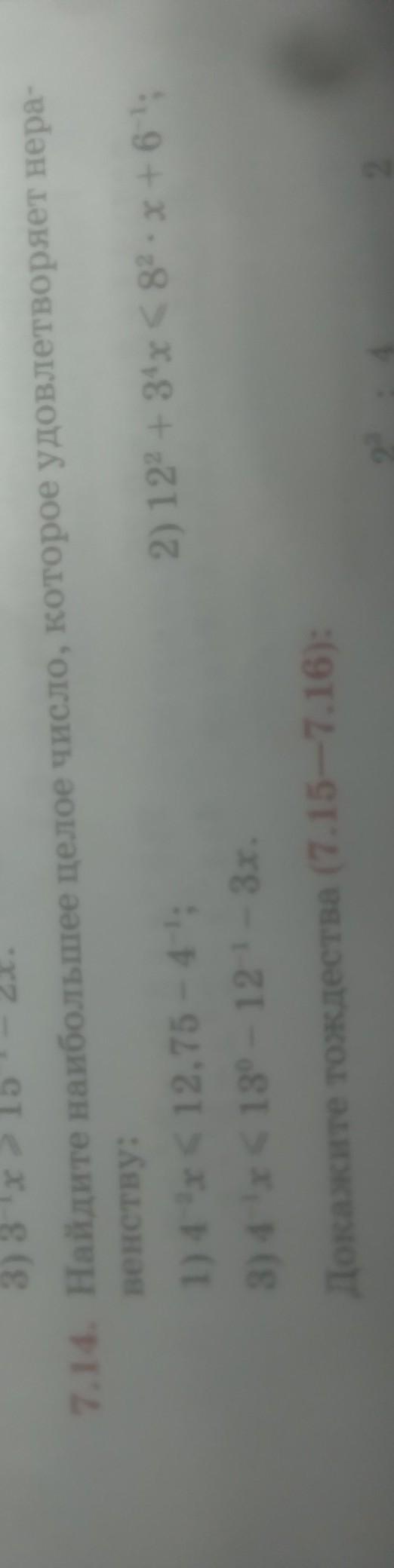
Ответы
Автор ответа:
0
№7,14
x ∈ ( -∞ ; 200 ]
наибольшее целое число, удовлетворяющее неравенству = 200
x ∈ ( -∞ ; ]
наибольшее целое число, удовлетворяющее неравенству = -8
x ∈ ( -∞ ; ]
наибольшее целое число, удовлетворяющее неравенству = 0
Похожие вопросы
Предмет: Русский язык,
автор: 55555193
Предмет: Русский язык,
автор: Spatars
Предмет: Английский язык,
автор: tedeevgamer
Предмет: Физика,
автор: sashashurikpetp1ha9g
Предмет: Русский язык,
автор: Fabien