Question

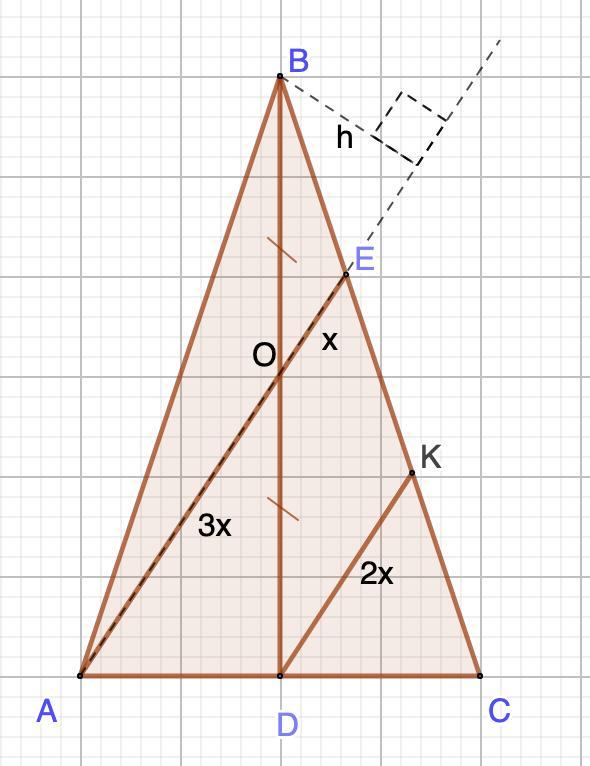
Дан равнобедренный треугольник ABC, (АВ=ВС). Точка 0- середина
высоты BD. Луч АО пересекает сторону ВС в точке Е. Найдите площадь треугольника
ВОЕ, если площадь треугольника ABC равна 72.

Answer 1

Ответ:

S=6 ед²

Объяснение:

Дано: ΔАВС - равнобедренный.

BO=OD

AO ∩ BC=E

S (ΔABC)=72

Найти: S (ΔBOE)

Решение:

Проведем DК || AE.

1. Рассмотрим ΔАВС - равнобедренный.

• В равнобедренном треугольнике высота является медианой.

⇒ BD - высота, медиана.

• Медиана делит треугольник на два равновеликих треугольника.

⇒S (ΔABD)=S (ΔDBC)=72:2=36.

2. Рассмотрим ΔABD.

DO=OB (условие)

⇒ АО - медиана

⇒ S (ΔAOD)=S (ΔAOB)=36:2=18.

3. Рассмотрим ΔDВК.

DО=ОВ; ОЕ || DК ⇒ ОЕ - средняя линия ΔDВК

• Средняя линия равна половине основания.

Пусть ОЕ=х, тогда DК=2х

4. Рассмотрим ΔАЕС.

АD=DС; DК || АЕ ⇒DК - средняя линия ΔАЕС.

DК=2х ⇒ АЕ = 4х

5.

Рассмотрим ΔАВО и ΔВОЕ.

АО=АЕ-ОЕ=4х-х=3х

$\displaystyle S_{ABO}=\frac{1}{2}AO*h=\frac{1}{2}*3xh=3\left(\frac{1}{2}xh\right)$

$\displaystyle S_{BOE}=\frac{1}{2} OE*h=\frac{1}{2}xh$

⇒ S (ΔAВО)=3S (ΔBOE)

$\displaystyle S_{ABO}=3S_{BOE}\\ \\ 18=3S_{BOE}\\\\S_{BOE}=6$