Предмет: Математика,
автор: tmusienko9
Помогите пожалуйста решить, чтобы было решение, Показательные неравенств 11
Приложения:
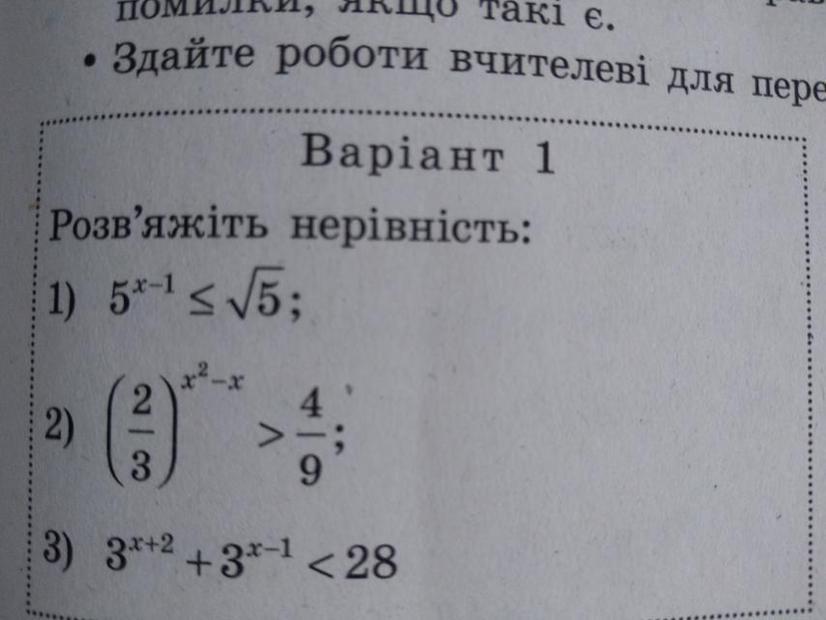
Ответы
Автор ответа:
1
Пошаговое объяснение:
Неравенства, которые в показателе степени содержат переменную, называются показательными.
Если а>1, то f(x) > g(x);
Если 0<a<1, то f(x) < g(x)
1)
x∈(-∞; 1,5]
2)
x∈(-1; 2)
3)
x∈(-∞; 1)
Похожие вопросы
Предмет: Русский язык,
автор: margo225ani
Предмет: Другие предметы,
автор: Vika070s
Предмет: Другие предметы,
автор: фатима122
Предмет: Математика,
автор: Angelina4746254
Предмет: Алгебра,
автор: izetova12