Question

помогите пожалуйста решить задание, с обьяснениями)

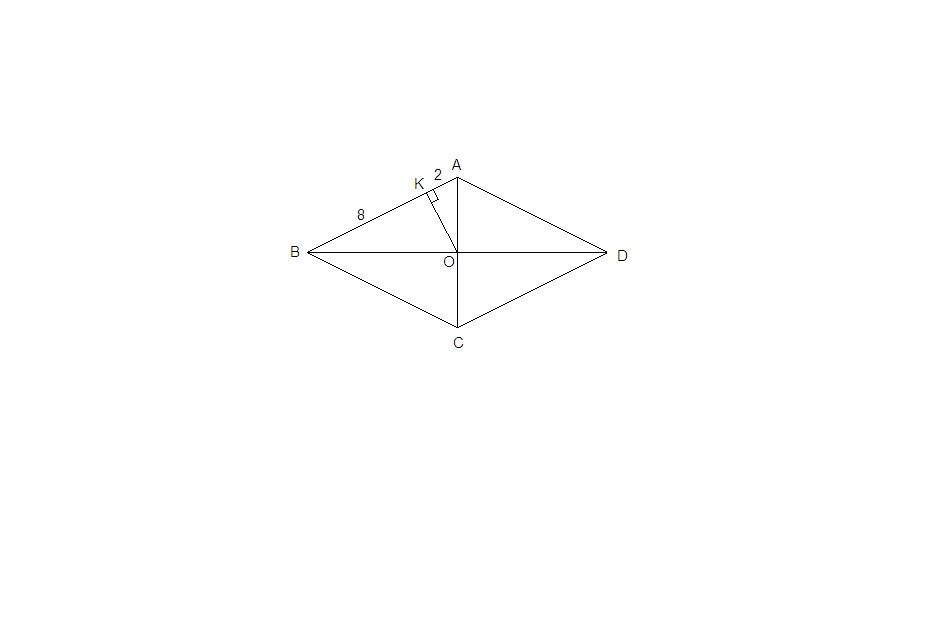
Диагонали ромба АВСД пересекаются в точке О. на стороне АВ взята точка К так, что ОК перпендикулярин АВ, АК=2см,ВК=8см. найдите диаганали ромба...

Answer 1

Диагонали ромба перпендикулярны и делятся точкой пересечения пополам.
ΔАОВ: ∠АОВ = 90°, ОК - высота прямоугольного треугольника, проведенная из вершины прямого угла.
Тогда по свойству пропорциональных отрезков  в прямоугольном треугольнике
ОК² = АК · КВ = 2 · 8 = 16
ОК = 4 см

ΔАОК: ∠АКО = 90°, по теореме Пифагора
           АО = √(АК² + ОК²) = √(4 + 16) = √20 = 2√5 см
АС = 2АО = 4√5 см

ΔВОК: ∠ВКО = 90°, по теореме Пифагора
           ВО = √(ВК² + ОК²) = √(64 + 16) = √80 = 4√5 см
BD = 2ВО = 8√5 см