Question

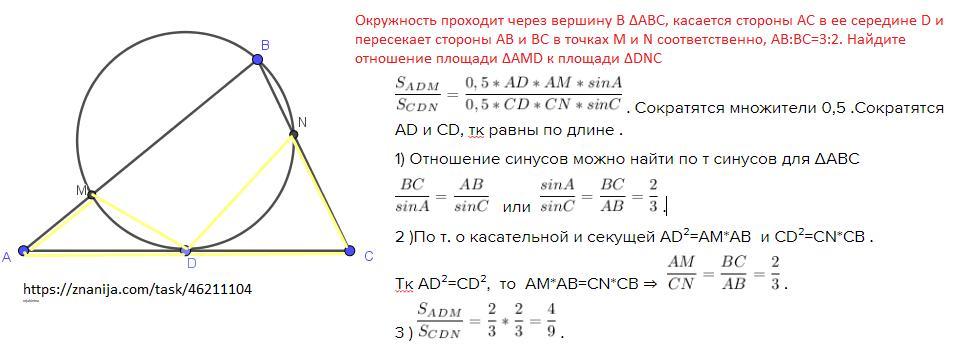
Окружность проходит через вершину B ΔABC, касается стороны AC в ее середине D и пересекает стороны AB и BC в точках M и N соответственно, AB:BC=3:2. Найдите отношение площади ΔAMD к площади ΔDNC

Answer 1

Окружность проходит через вершину B ΔABC, касается стороны AC в ее середине D и пересекает стороны AB и BC в точках M и N соответственно, AB:BC=3:2. Найдите отношение площади ΔAMD к площади ΔDNC

Объяснение:

$\displaystyle \frac{S_A_D_M}{S_C_D_N} =\frac{0,5*AD*AM*sin A}{0,5*CD*CN*sinC}$ . Сократятся множители 0,5 .Сократятся  AD и CD, тк равны по длине .

1) Отношение синусов можно найти по т синусов для ΔАВС

$\displaystyle \frac{BC}{sinA} =\frac{AB}{sinC}$   или  $\displaystyle \frac{sinA}{sinC} } =\frac{BC}{AB} =\frac{2}{3}$ .

2 )По т. о касательной и секущей АD²=AM*AB  и СD²=CN*CB .

Тк АD²=СD²,  то  AM*AB=CN*CB ⇒  $\displaystyle \frac{AM}{CN} =\frac{BC}{AB} =\frac{2}{3}$ .

3 ) $\displaystyle \frac{S_A_D_M}{S_C_D_N} =\frac{2}{3} *\frac{2}{3} =\frac{4}{9}$ .