Question

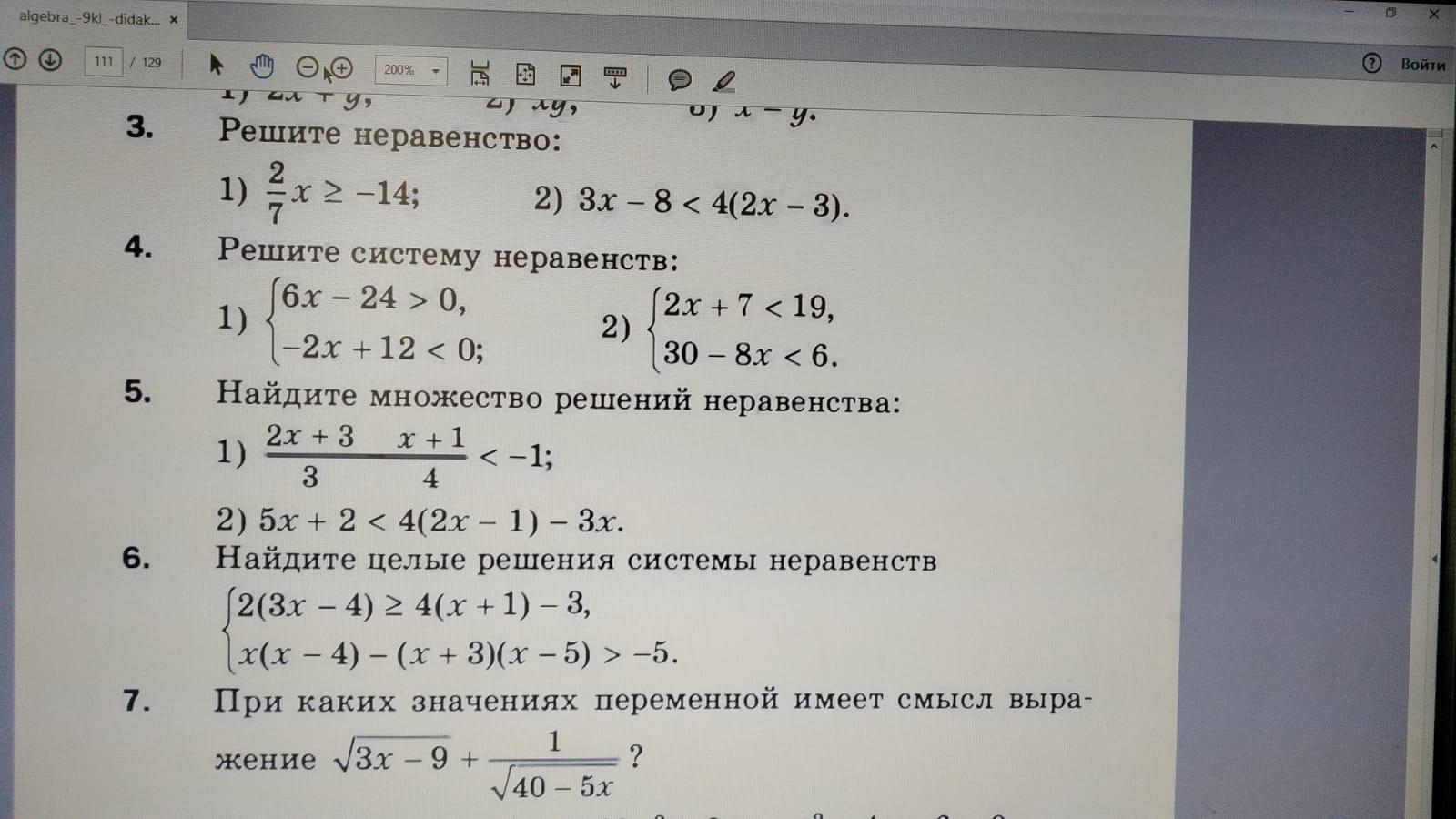
Пожалуйста, помогите с 3 заданием!!!

Answer 1

Ответ:вот 3 задание

Объяснение:

Answer 2

Ответ:

$\large{1) \:\:{x \geqslant - 49 }\: }\small{{или}\: } \: \large{ x \in [ - 49 ; \: + \infty )} \\ \large{2) \:\:{x > 0.8} \: }\: \small{или} \: \: \large{x \in (0.8; + \infty )} \quad$

Объяснение:

Зад. 3 п.1)

$\frac{2}{7} x \geqslant - 14 \: \bigg | \: \small{ { \times} \tfrac{7}{2} > 0 }\\ \frac{7}{2} \cdot \frac{2}{7} {\cdot }x \geqslant \frac{7}{2} \cdot ({ - 14}) \\ 1 \cdot x \geqslant - 7 \cdot 7 \\ x \geqslant - 49 \: \: < = > x \in [ - 49 ; \: + \infty )$

Зад.3 п.2)

$3x - 8 < 4(2x - 3)$

Раскроем скобки справа

$3x - 8 < 4 {\cdot}2x - 4 {\cdot}3 \\ 3x - 8 < 8x - 12$

Для удобства перепишем "наоборот", поменяв правую и левую части (знак неравенства тоже изменяем на обратный)

$8x - 12 > 3x - 8 \\ 8x - 3x > - 8 + 12 \\ 5x > 4 \: \: {< = }{> } \: \: \: x > \frac{4}{5} \\ x > 0.8 \: \: \: { < = }{ > } \: \: \: \: x \in (0.8; + \infty )$