Question

Геометрия соч 9 класс
задание 2
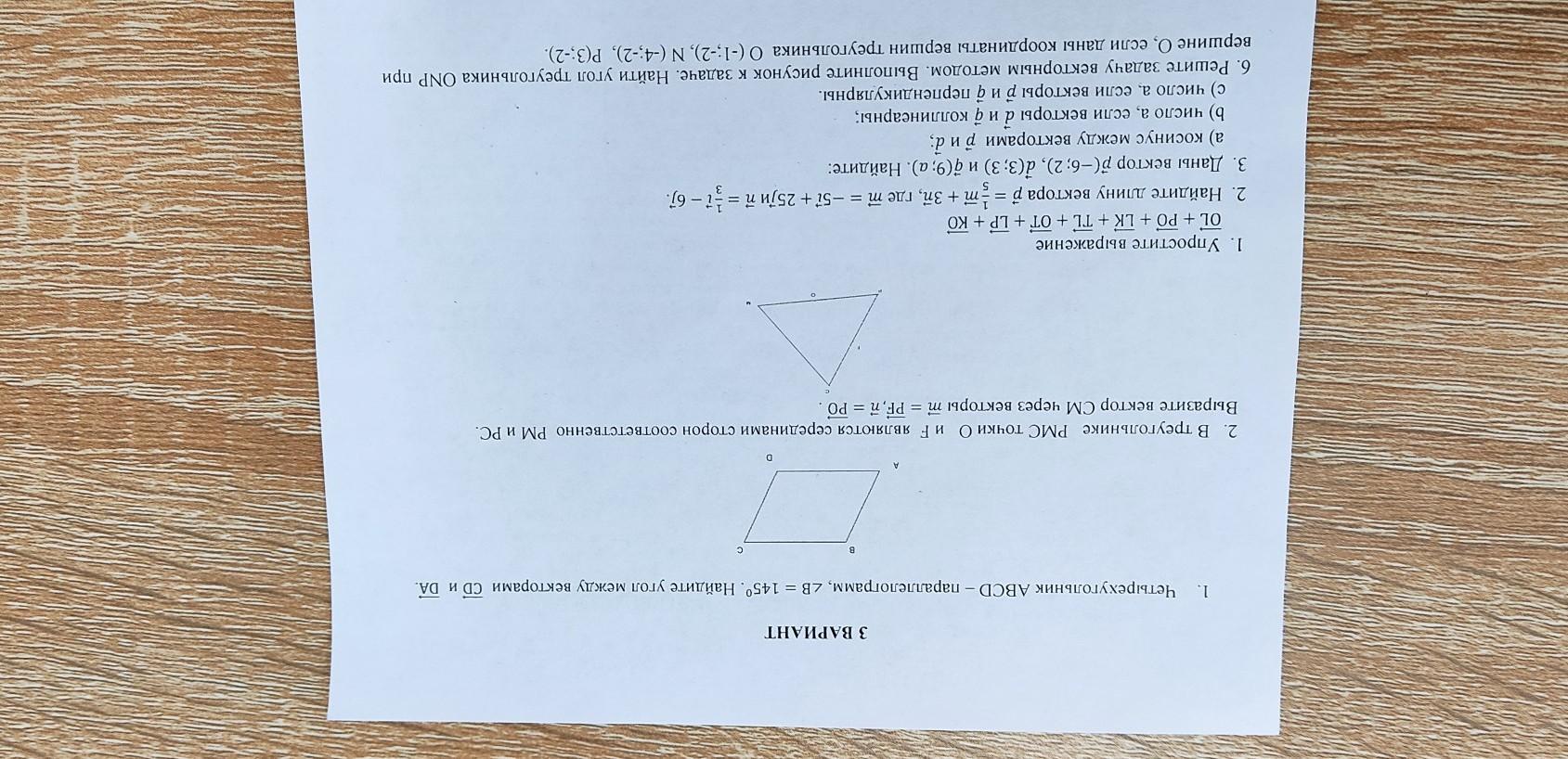
В треугольнике РМС точки О и F являются серединами сторон соответственно РМ и PC.

Выразите вектор СМ через векторы м = PE, n = PO
задание 3
задание 4​

Answer 1

Объяснение:

2.

Дано: ΔРСМ;

PF=FC; PO=OM

$\overrightarrow{PF}= \overrightarrow{m};\;\;\;\overrightarrow{PO}=\overrightarrow{n}$

Выразить вектор СМ через векторы m и n.

Решение:

Так как точки F и O - середины отрезков РС и РМ соответственно, то

$\overrightarrow{PC}=2\overrightarrow{PF}=2\overrightarrow{m} \\\\\overrightarrow{PM}=2\overrightarrow{PO}=2\overrightarrow{n}$

По правилу треугольника:

$\overrightarrow{PM} =\overrightarrow{PC}+\overrightarrow{CM} \\\\\Rightarrow \;\overrightarrow{CM}=\overrightarrow{PM} -\overrightarrow{PC} =2\overrightarrow{n}-2\overrightarrow{m}$

3.

Дано:

$\overrightarrow{p}(-6;2),\;\overrightarrow{d}(3;3),\;\overrightarrow{q}(9;a).$

a) $\overrightarrow{p}(-6;2),\;\overrightarrow{d}(3;3)$

$\displaystyle cos\phi=\frac{x_px_d+y_py_d}{\sqrt{x_p^2+y_p^2 } *\sqrt{x_d^2}+y_d^2 }\\\\\frac{-6*3+2*3}{\sqrt{36+4}*\sqrt{9+9} } =\frac{-12}{2\sqrt{10}*3\sqrt{2} } =\frac{-12}{12\sqrt{5} } =-\frac{1}{\sqrt{5} } \approx -0,45$

b) $\overrightarrow{d}(3;3),\;\overrightarrow{q}(9;a).$

Векторы коллинеарны если:

$\displaystyle \frac{x_d}{x_q}=\frac{y_d}{y_q}\\\\ \frac{3}{9}=\frac{3}{a}\;\;\;\Rightarrow \;\;\;a=\frac{9*3}{3} =9$

c) $\overrightarrow{p}(-6;2),\;\overrightarrow{q}(9;a).$

Векторы перпендикулярны, если скалярное произведение равно нулю.

$\overrightarrow{p}*\overrightarrow{q}=0$

$\overrightarrow{p}*\overrightarrow{q}=x_px_q+y_py_q\\\\-6*9+2a=0\\2a=54\\a=27$