Question

Помогите пожалуйста с 4 задачей по геометрии ​

Answer 1

Ответ:

V=48√3(ед³)

Объяснение:

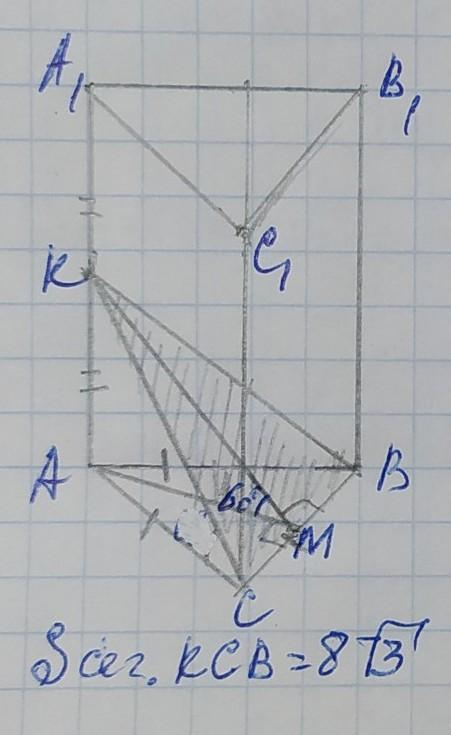
Обозначим вершины призмы АВСА₁В₁С₁ с основанием АВС, точкой К – середину ребра АА₁, тогда сечение СВК. Проведём перпендикуляры КМ и АМ стороне ВС. Оба перпендикуляра совпадают в точке М, так как ∆АВС – равносторонний, то АМ является также медианой, поэтому делит сторону ВС пополам. ∆СКВ равнобедренный, так как призма правильная, то КС=КВ, и высота КМ так же является медианой. Точка М – это середина стороны ВС. Получим ∠АМК=60°, который является линейным углом между плоскостями – сечения СВК и основанием призмы АВС. Так как призма правильная, то в её основании лежит равносторонний треугольник. В равностороннем треугольнике все стороны равны, обозначим их а, тогда АВ=ВС=АС=а. Найдём высоту АМ в ∆АВС. Высота равностороннего треугольника вычисляется по формуле:

АМ=а√3/2. Рассмотрим ∆АКМ. Он прямоугольный, в котором АК и АМ – катеты, а КМ – гипотенуза. Найдём гипотенузу КМ через косинус угла. Косинус угла – это отношение прилежащего к углу катета к гипотенузе, поэтому:

cos AMK=AM/KM

KM×cosAMK=AM

KM×cos60°=а√3/2

KM×1/2=а√3/2

KM=а√3/2÷1/2

KM=2×а√3/2

KM=а√3

Найдём площадь сечения – ∆СКВ. Площадь треугольника вычисляется по формуле:

S=ВС×КМ/2=а×а√3/2=а²√3/2(ед²)

По условию площадь сечения равна 8√3(ед²), приравняем:

а²√3/2=8√3

а²=8√3÷√3/2

а²=8√3×2/√3

а²=16√3÷√3

а²=16

а=√16

а=4 – сторона основания.

тогда АМ=а√3/2=4√3/2=2√3,

КМ=а√3=4√3

Sabc=BC×AM/2=4×2√3/2=4√3(ед²)

В ∆АКМ найдём АК по теореме Пифагора:

АК²=КМ²–АМ²=(4√3)²–(2√3)²=16×3–4×3=

=48–12=36

АК=√36=6

Так как АК=КА₁, то АА₁=АК+КА₁=6+6=12

V=Sabc×AA₁=4√3×12=48√3(ед³)