Предмет: Алгебра,
автор: bftvvhtrgh
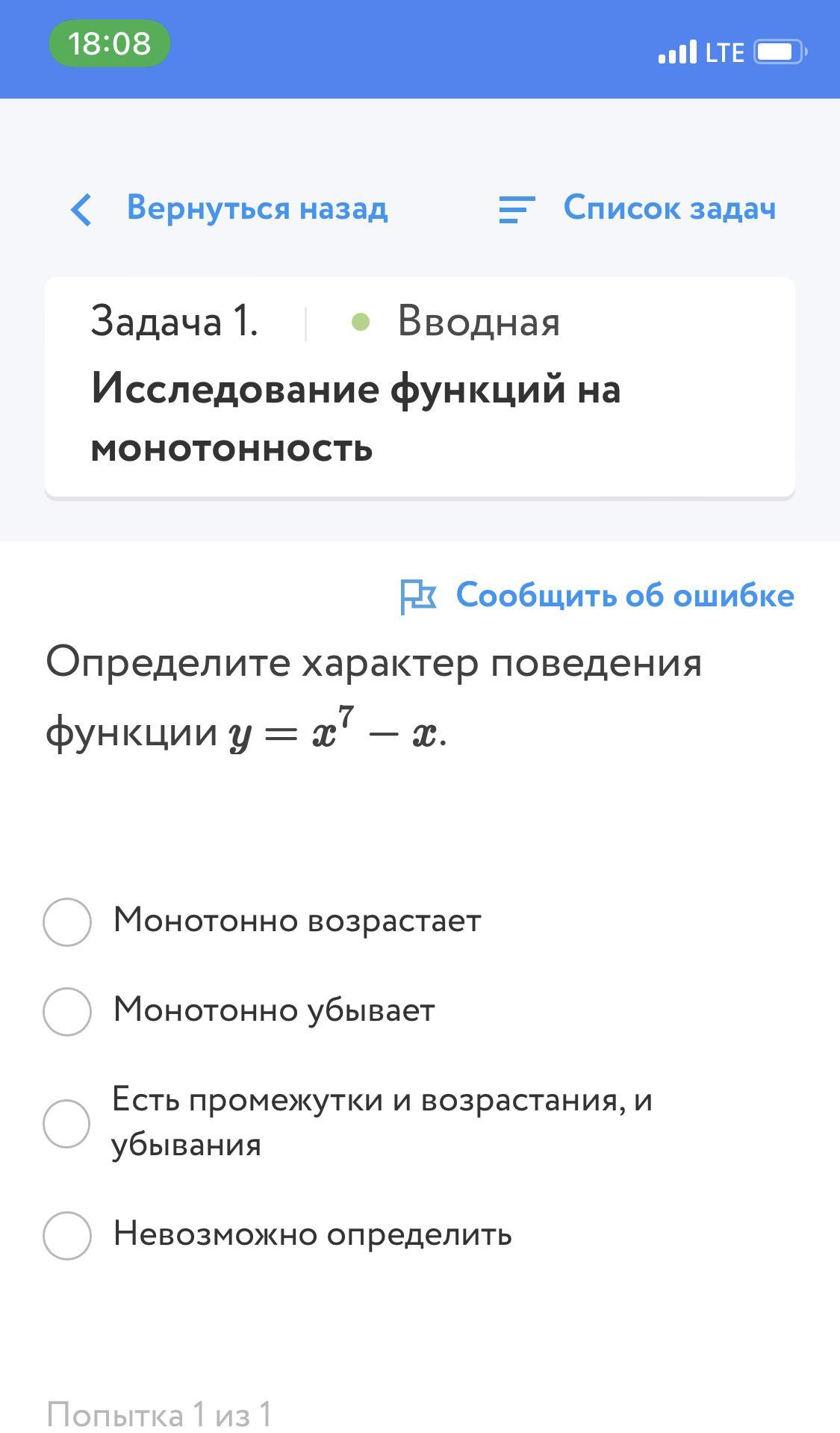
Решить одну задачку.
Приложения:
Ответы
Автор ответа:
0
Ответ:
Есть промежутки и возрастания при и убывания при
.
Похожие вопросы
Предмет: Английский язык,
автор: ДаниилРушинский
Предмет: Русский язык,
автор: vikamileyko
Предмет: Русский язык,
автор: МарьянаШ
Предмет: Физика,
автор: gmasmalinin
Предмет: Алгебра,
автор: Svetkoooo