Question

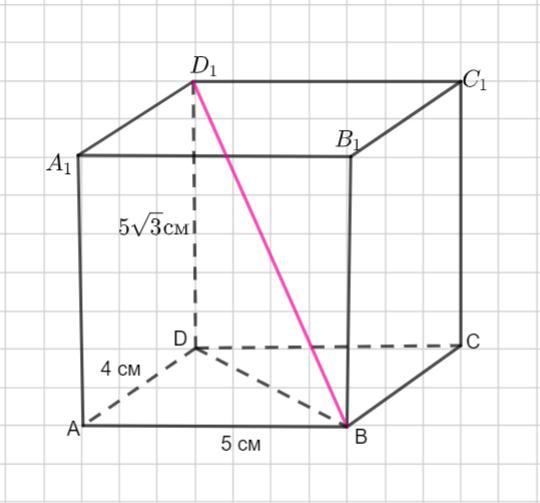
В прямом параллелепипеде стороны основания равны 4см и 5см, а один из углов равен 120°. Высота призмы равна 5√3 см. Выполните рисунок по условию задачи
а) Найдите меньшую диагональ параллелепипеда
б) Вычислите площадь полной поверхности параллелепипеда

Answer 1

Ответ:

а) $4\sqrt{6}$ см;  б) $110\sqrt{3}$  см ².

Объяснение:

Рассмотрим прямой параллелепипед $ABCDA_{1} B_{1} C_{1} D_{1}$

AB= 5 см ,   AD=  4 см.

Высота $DD_{1}=5\sqrt{3}$ см.

∠D=120°.

а) Сумма ∠А+∠D=180°, так как это односторонние углы при  AB║CD и секущей AD.

Тогда ∠А=180°-120°=60°.

Найдем BD -меньшую диагональ основания по теореме косинусов:

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Рассмотрим треугольник Δ ABD.

$BD ^{2} =AD^{2} +AB ^{2} -2\cdot AD\cdot A B\cdot cos A;\\BD ^{2} =4^{2} +5^{2} -2\cdot 4 \cdot5\cdot cos60^{0} ;\\BD ^{2} =16+25-2\cdot20\cdot \dfrac{1}{2} =16+25-20=21;\\BD=\sqrt{21} .$

Диагональ $BD{_1}$ параллелепипеда наименьшая, так как она опирается на наименьшую диагональ основания.

Рассмотрим Δ $D{_1}DB$ - прямоугольный.

Найдем гипотенузу $BD{_1}$ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$BD{_1}^{2} =D{_1}D^{2} +BD^{2} ;\\BD{_1}=\sqrt{D{_1}D^{2} +BD^{2}} ;\\BD{_1}=\sqrt{(5\sqrt{3} )^{2} +(\sqrt{21} )^{2} } =\sqrt{75+21} =\sqrt{96} =\sqrt{16\cdot 6} =4\sqrt{6}$

$BD{_1}=4\sqrt{6}$ см.

б) Найдем площадь поверхности параллелепипеда как сумму площади боковой поверхности и удвоенной площади основания.

Найдем площадь основания параллелепипеда по формуле:

$S=a\cdot b \cdot sin\alpha ,$  где α - угол между сторонами.

$S=4\cdot 5 \cdot \sin 60^{0} =20\cdot \dfrac{\sqrt{3} }{2} =10\sqrt{3}$  

Тогда площадь основания параллелепипеда равна $10\sqrt{3}$ см².

Площадь боковой поверхности найдем как произведение периметра основания на высоту.$S=2\cdot(4+5)\cdot 5\sqrt{3} =2\cdot9\cdot 5\sqrt{3} =90\sqrt{3}$  см ².

Тогда площадь полной поверхности будет:

$S= 90\sqrt{3} +2\cdot 10\sqrt{3} =90\sqrt{3} +20\sqrt{3} =110\sqrt{3}$ см².