Предмет: Алгебра,
автор: DonSERG
Продифференцировать функцию и найти значение производной функции в точке x0
Приложения:
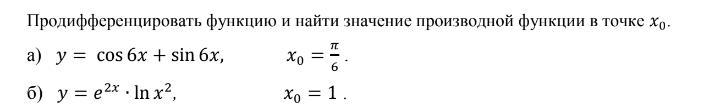
Ответы
Автор ответа:
1
Ответ:
Объяснение:
а)
б)
DonSERG:
cgfcb,j
спасибо!
Помогите решить последнюю задачу( у меня в вопросах) ник Mishka1239
Похожие вопросы
Предмет: Русский язык,
автор: лиля180
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: элька00001
Предмет: Английский язык,
автор: sn2001191200115