Предмет: Математика,
автор: RuslanRussia1881
Математика помогите пожалуйста
Приложения:
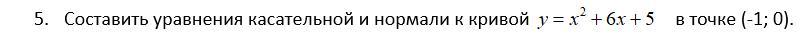
Ответы
Автор ответа:
1
Пошаговое объяснение:
Уравнение касательной:
Уравнение нормали:
Найдем производную:
Найдем у(х₀) и у'(x₀):
Составим уравнение касательной:
Составим уравнение нормали:
Похожие вопросы
Предмет: Английский язык,
автор: asadfbnv
Предмет: Русский язык,
автор: дениска60
Предмет: Русский язык,
автор: Kozha11
Предмет: Английский язык,
автор: nadya3426276
Предмет: Математика,
автор: neverevergot7