Question

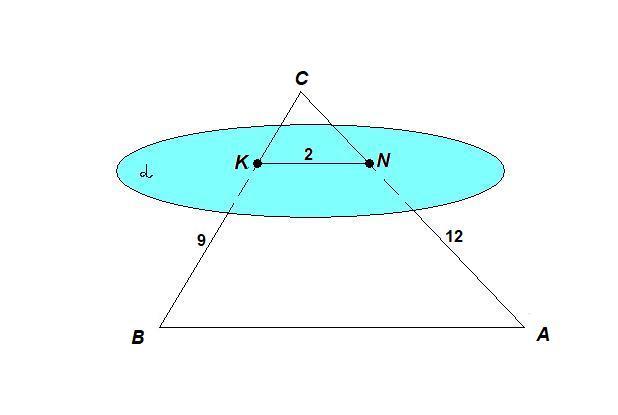
ABC стенка Ab треугольника параллельная плоскость пересекается с его стенками AC и BC в точках N,K соответственно.Известно, что NK=2м AN=12м.AC=16м BK=9м .Найдите длины ребер AB и BC

Answer 1

Ответ:

АВ = 8 м

ВС = 12 м

Объяснение:

AB║α, плоскость (АВС) проходит через прямую, параллельную плоскости α, значит линия пересечения параллельна АВ,

NK║AB.

∠CNK = ∠CAB как соответственные при пересечении параллельных прямых АВ и NK секущей АС,

∠С - общий для треугольников CNK и САВ, значит

ΔCNK ~ ΔCAB по двум углам.

$\dfrac{AB}{NK}=\dfrac{BC}{KC}=\dfrac{AC}{NC}$

NC = AC - AN = 16 - 12 = 4 м

$\dfrac{AB}{NK}=\dfrac{AC}{NC}$

$\boldsymbol{AB}=\dfrac{NK\cdot AC}{NC}=\dfrac{2\cdot 16}{4}=2\cdot 4\boldsymbol{=8}$  м

$\dfrac{BC}{KC}=\dfrac{AC}{NC}$

$\dfrac{BK+KC}{KC}=\dfrac{AC}{NC}$

$\dfrac{9+KC}{KC}=\dfrac{16}{4}=4$

$9 + KC = 4KC$

$3KC = 9$

$KC = 3$ м

ВС = ВК + КС = 9 + 3 = 12 м