Предмет: Алгебра,
автор: ruslan1087
Сколько корней имеет и решить (x^2-5)*(x+√-x)=0
Ответы
Автор ответа:
1
Ответ:
2 корня
Объяснение:
Решение на фото.
Приложения:
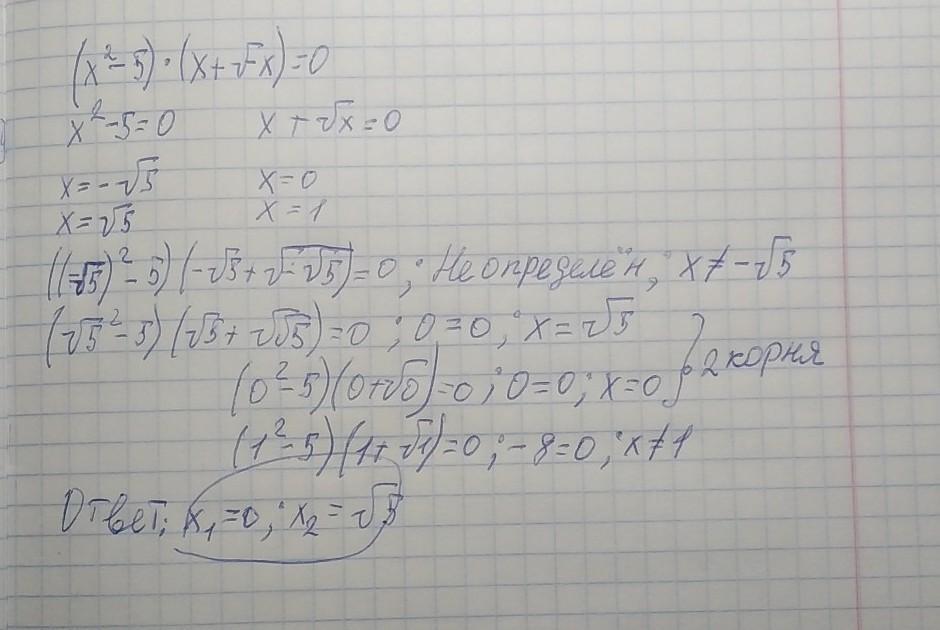
qtyblox587:
какой 3 корень?
те два корня которые ты написал и еще x=-1
когда мы делим два уравнения на 4 части нужно чтобы там 2 части были равны например 0=0 это правильное и оно нам подходит, и это будет являться корнем а если - 8=0 то оно не будет являться корнем т.к. обе части не равны
так
что в. итоге
в данном случае у нас даны 4 корня которых нужно определить являются они корнем данного уравнения или нет? в 1 нет во 2 да т.к 0=0 в 3 да т.к0=0 4 нет т.к-8=0
чел сделал и у него 3 корня
ты ошибаешься
понимаешь
можешь посмотреть как он решил
Автор ответа:
0
Ответ: х=0; х=-1; х=-√5
Объяснение:(x²-5)*(x+√-x)=0- ПРОИЗВЕДЕНИЕ равно нулю. при условии, что одна из скобок равна нулю. при этом вторая существует.
а)если
x²-5=0, то х²=5; х=±√5, при х=√5 не существует √-x=√(-√5), поэтому х=√5- лишний корень.
б) если же x+√-x=0, при этом ОДЗ уравнения -х≥0, х≤0; получим √-х*(1+√(-х))=0⇒х=0 ; х=-1 оба корня входят в ОДЗ уравнения и при этих значениях первая скобка существует.
в) Вывод : корнями исходного уравнения являются
х=0; х=-1; х=-√5
Похожие вопросы
Предмет: Английский язык,
автор: Паровм
Предмет: Русский язык,
автор: Diduo
Предмет: Русский язык,
автор: alekseichuktatj1
Предмет: Физика,
автор: 54fedase
Предмет: Английский язык,
автор: ilchuk