Предмет: Алгебра,
автор: zhasulanasanov69
...............орлраапргрпп
Приложения:
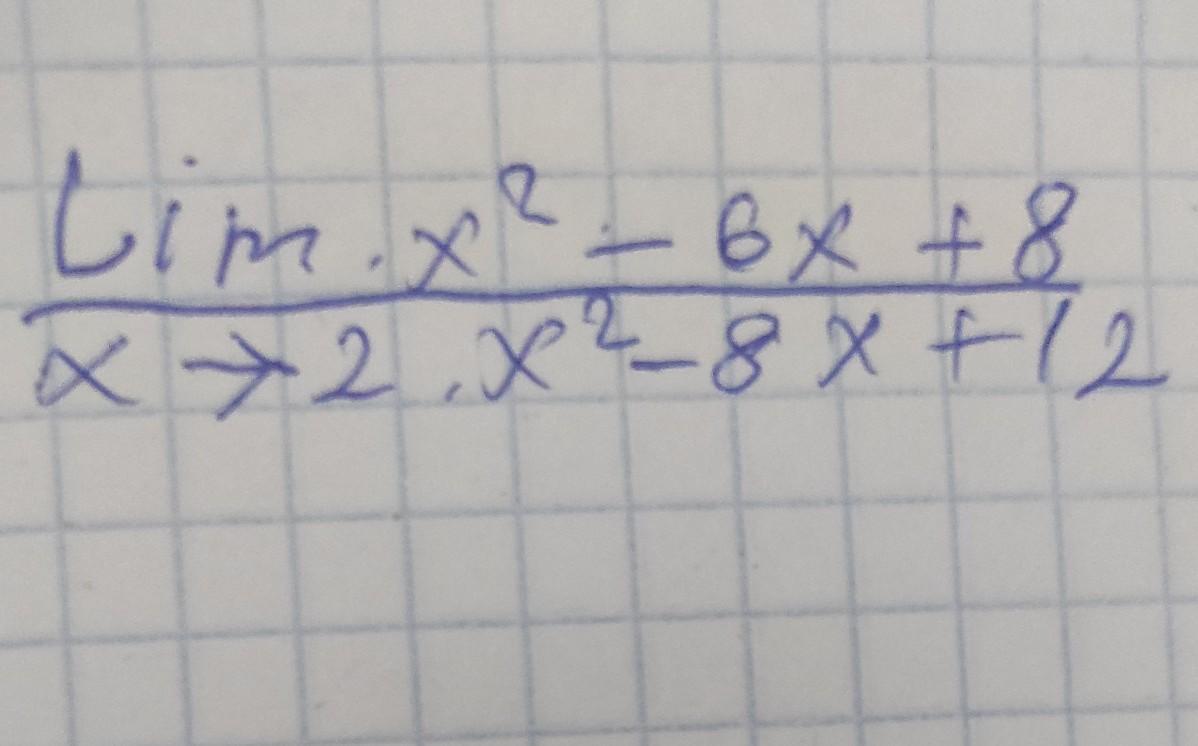
Ответы
Автор ответа:
0
Ответ:
Объяснение:
- неопределенность
множители я нашел устно по теореме Виета и одному правилу
Похожие вопросы
Предмет: Русский язык,
автор: сая05
Предмет: Английский язык,
автор: novozhilovvano
Предмет: Русский язык,
автор: saidova2
Предмет: Музыка,
автор: 5432881
Предмет: Физика,
автор: svitlana122