Предмет: Алгебра,
автор: Алина3456
помогите вычислить интеграл с помощью формул понижения степени
Приложения:
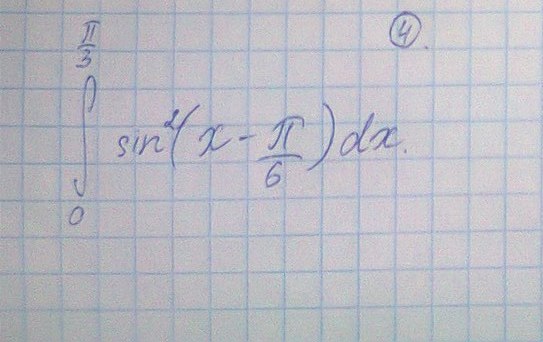
Ответы
Автор ответа:
0
Автор ответа:
0
у меня только почему-то П/6-корень из3/8 получилось...
Автор ответа:
0
Там двойки сокращаются, и остаётся(1/4)*(V3/4)=V3/4.
Автор ответа:
0
sin^2(x-pi/6)=(1-cos2(x-pi/6))/2=1/2-cos2(x-pi/6) интеграл(1./2)-интеграл(cos(x-pi/6)/2) =1/2x|(0 pi/3)-sin(x-pi/6)/2 (0 pi/3)=1/2(pi/3-0)-1/2sin(pi/3-pi/6)+1/2sin(0-pi/6=pi/6-1/2*1/2+1/2*1/2=pi/6
Похожие вопросы
Предмет: Русский язык,
автор: aminakazarova7
Предмет: Информатика,
автор: evgenijnikolaenko71
Предмет: Английский язык,
автор: yaroslavtasher2007
Предмет: Математика,
автор: hamster212
Предмет: Биология,
автор: LenaLena12345