Question

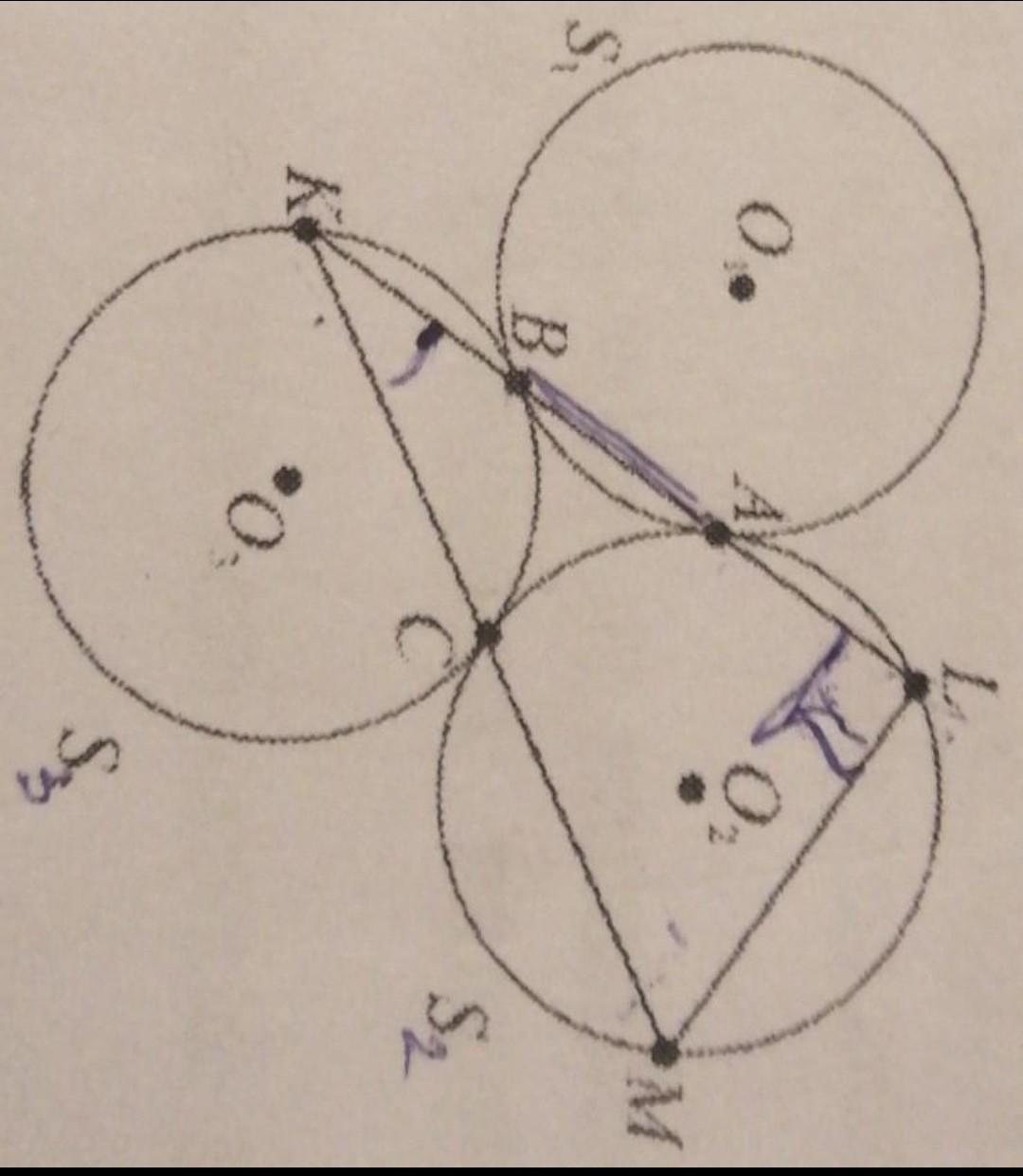
Три равные окружности S1, S2, S3 попарно касаются друг друга: S1 и S2 в точке A, S1 и S3 в точке B, S2 и S3 в точке C. Прямая AB пересекает окружность S3 в точке K и окружность S2 в точке L. Прямая KC пересекает окружность S2 в точке M. Докажите, что треугольник KLM прямоугольный​

Answer 1

Ответ:

Пусть окружности S1 и S2 касаются в точке A, S2 и S3 -- в точке B, S1 и S3 — в точке C; O1, O2, O3 — центры этих окружностей.

Если прямые AB и AC пересекают окружность S3 соответственно в точках M и N (отличных от B и C), то равнобедренные треугольники AO1C и NO3C имеют равные углы при вершине C. Поэтому их углы при вершинах A и N также равны. Следовательно, O3N || O1A. Аналогично O3M || O2A.

Точка A лежит на прямой O1O2. Поэтому O3N || O1O2 и O3M || O1O2. Следовательно, прямая MN проходит через центр O3 третьей окружности.

Объяснение: