Предмет: Алгебра,
автор: jofaropkil
освободиться от иррациональности в знаменателе.
1)7/√b-√a
2)3-a/√3-a
3)1/2√b
Если что /-дробь
Ответы
Автор ответа:
1
Ответ:
Смотри решение на фото ниже
Приложения:
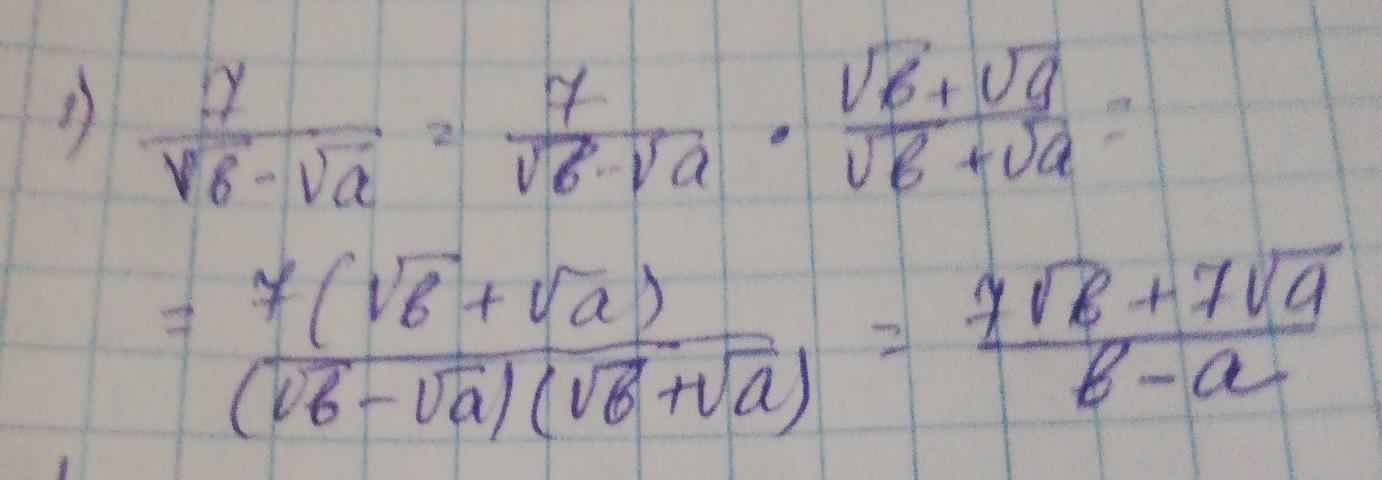
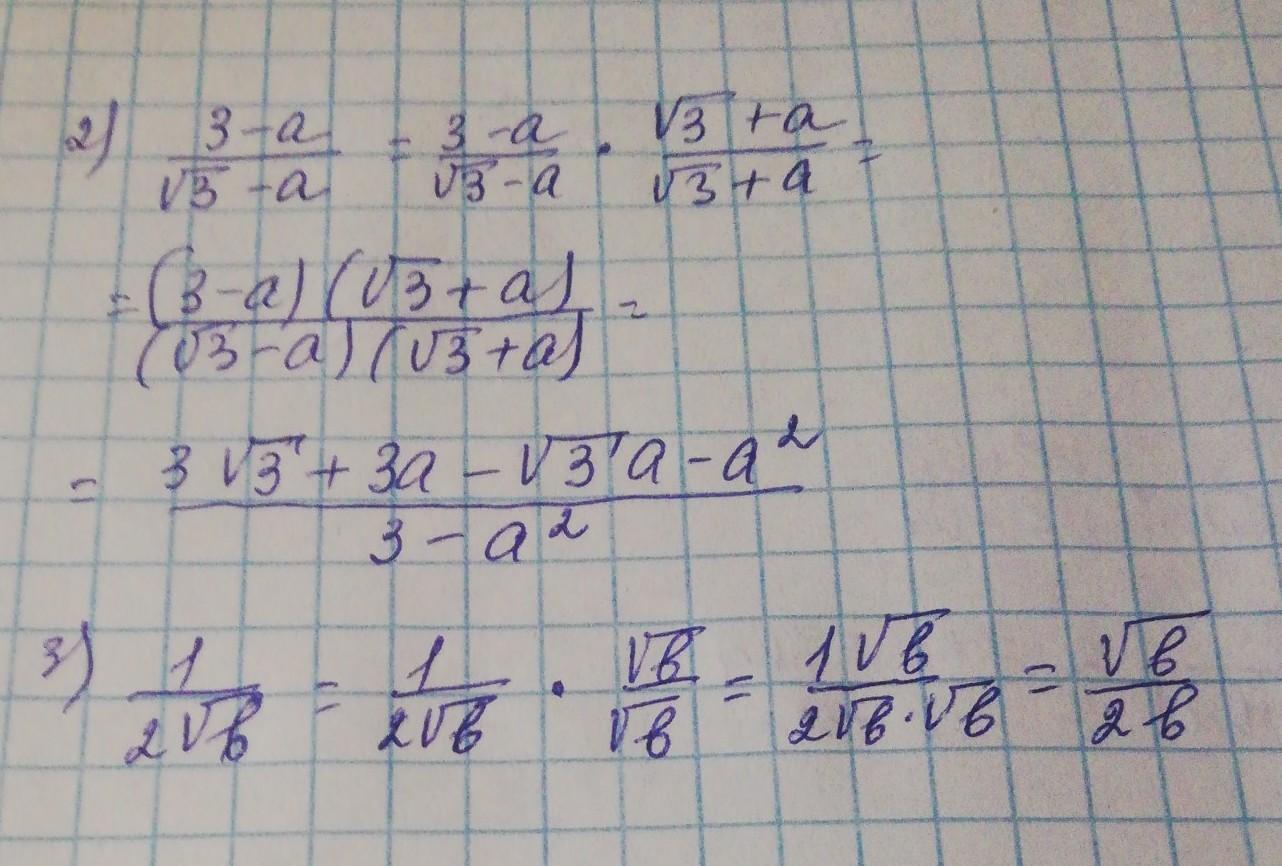
larisaserova53:
2)примпр в знаменателе под корнем все выражение или только корень из 3?
только корень из 3
Посмотрите примеры все правильно записаны, я правильно поняла?
побыстрее, а то не смогу исправить!!
да
ну все тогда!
спасибо тебе
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: esma001
Предмет: Математика,
автор: mudrikdasa