Предмет: Алгебра,
автор: stadnikarina11
Даю 100!!!!!!!!!!!!!!!!!!!!! срочно!!!!!!!!!!!
Приложения:
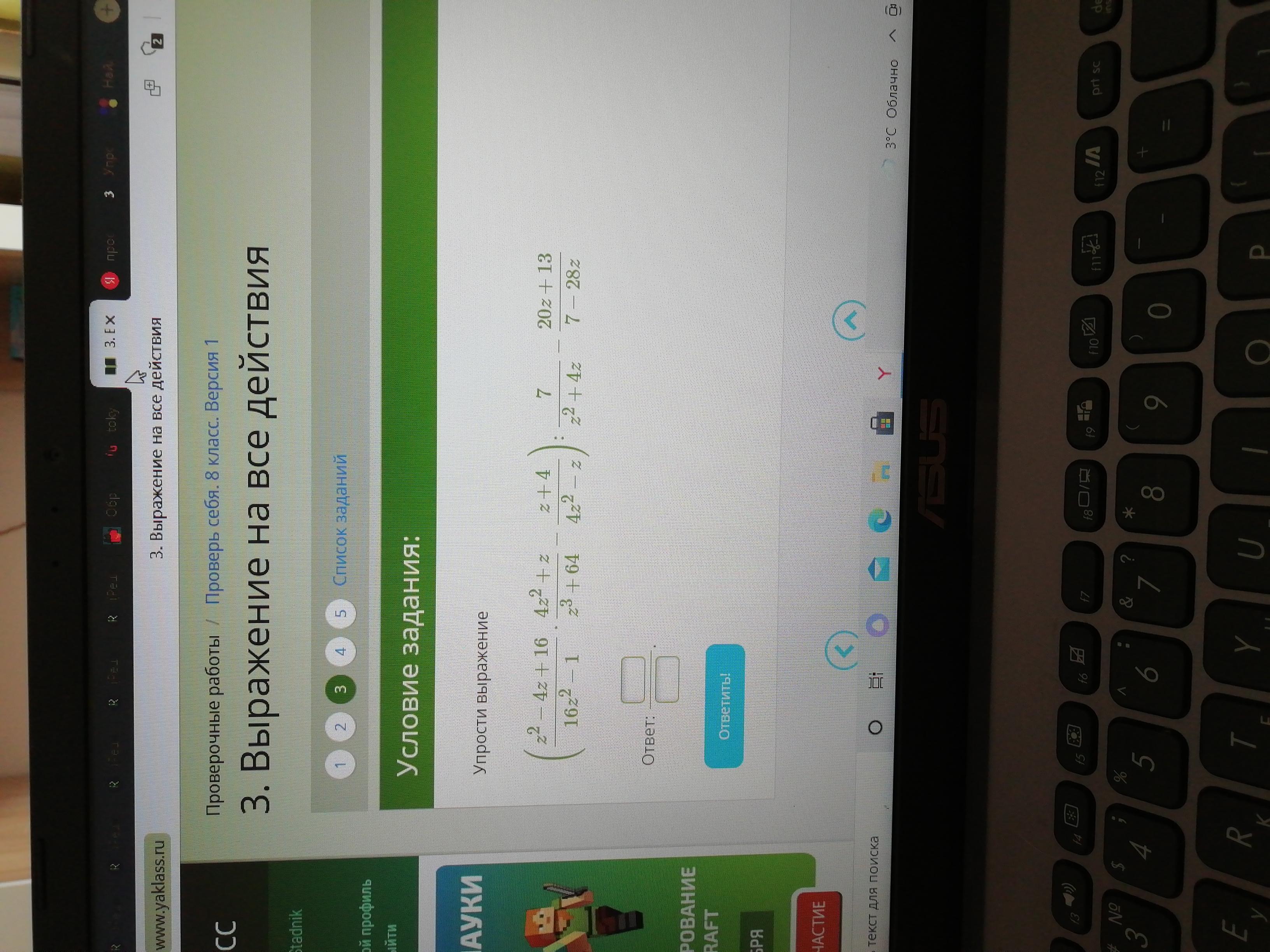

Ответы
Автор ответа:
1
=
Похожие вопросы
Предмет: Русский язык,
автор: меллори
Предмет: Русский язык,
автор: hahahahahaha5555555
Предмет: Русский язык,
автор: LanaBoo
Предмет: Алгебра,
автор: OrumDayn
Предмет: Геометрия,
автор: ebolibobo