Предмет: Алгебра,
автор: bbxbzhuzsyywuwy
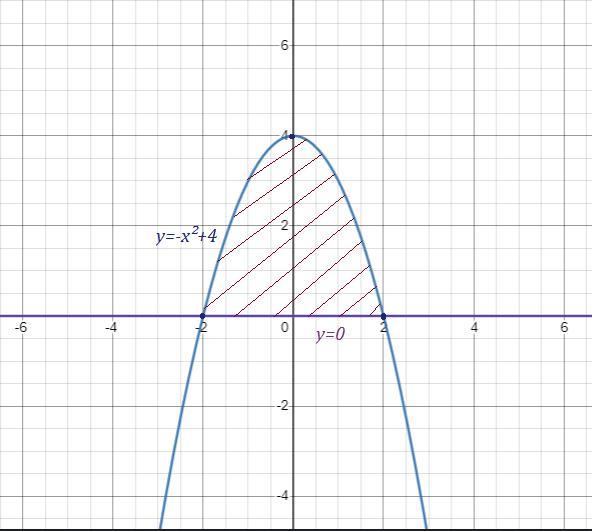
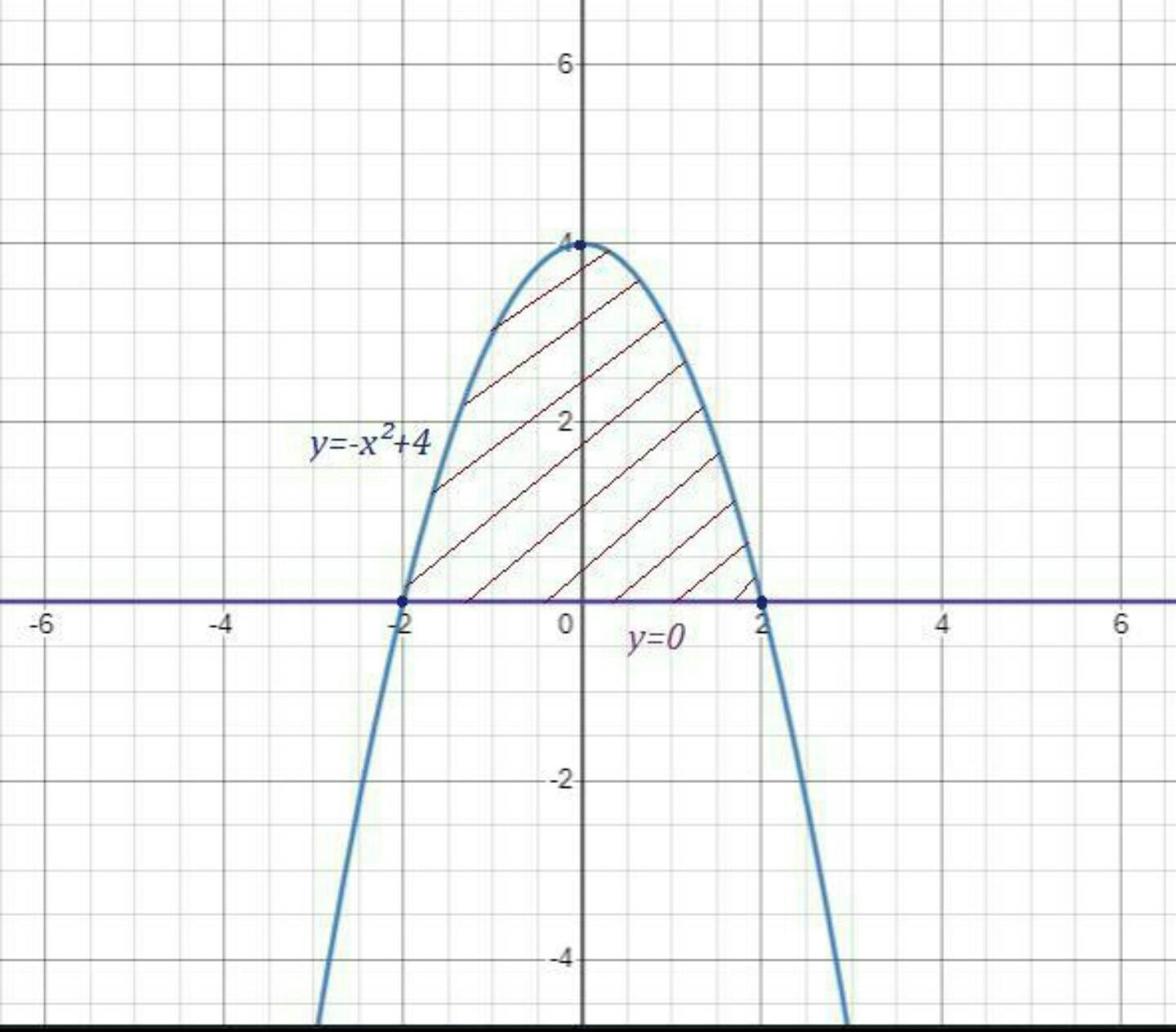
Найти площадь фигуры ограниченной линиями y=-x^2+4
Y=0
Ответы
Автор ответа:
0
Ответ:
Приложения:
Автор ответа:
0
Ответ:
jfh Josh will be there in about the new one you have
Приложения:
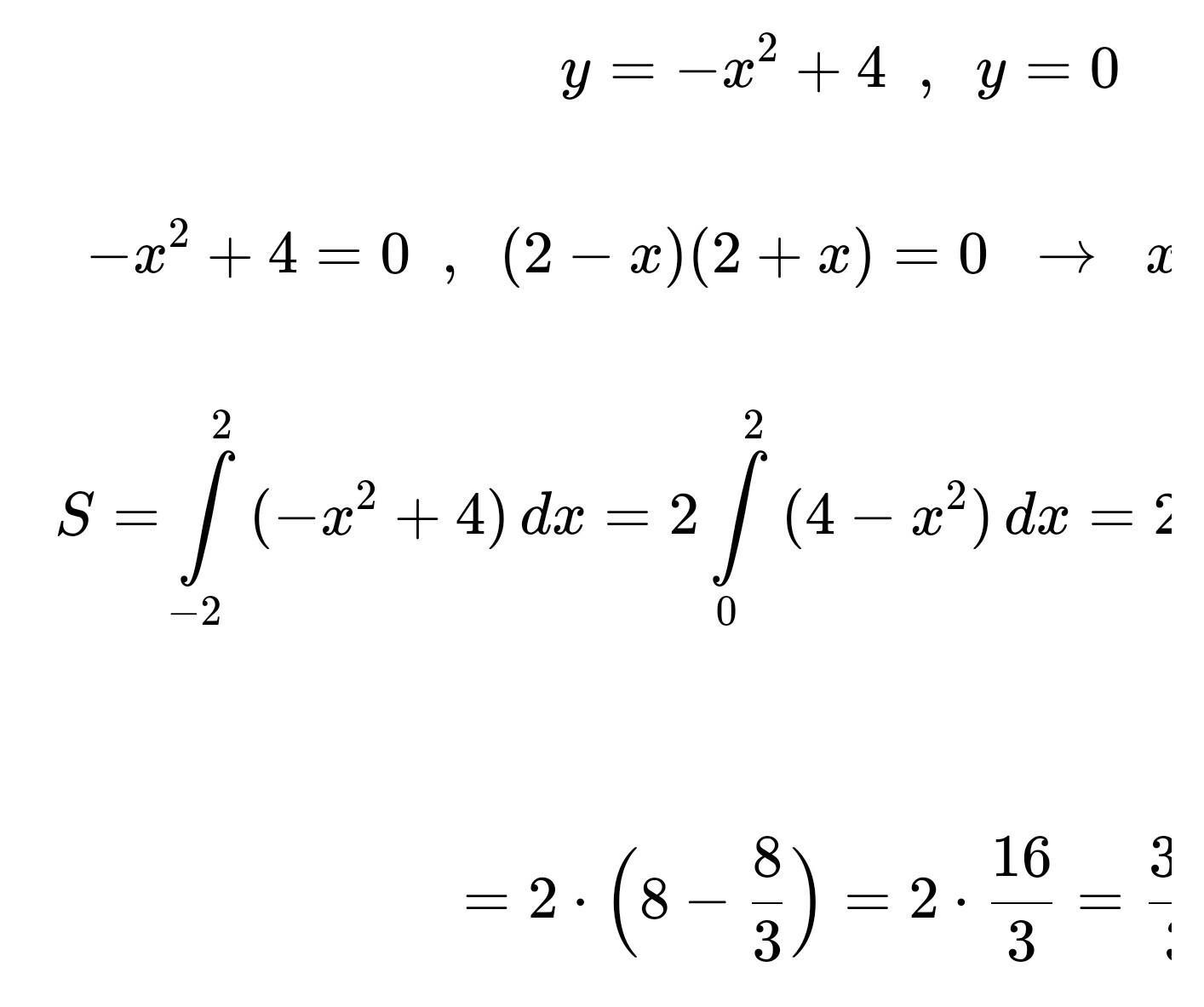
Похожие вопросы
Предмет: Окружающий мир,
автор: Аоаолоонгдо
Предмет: Английский язык,
автор: соня582
Предмет: Другие предметы,
автор: JavaMineCraft
Предмет: Русский язык,
автор: Payman
Предмет: Математика,
автор: Lerka200387