Question

Из единичных кубиков собрали большой куб. Два кубика будем называть соседними, если они соприкасаются гранями. Таким образом, у одного кубика может быть до 6 соседей. Известно, что количество кубиков, у которых ровно 4 соседа, равно 156. Найдите количество кубиков, у которых ровно 5 соседей.​

Answer 1

Ответ: 726 кубиков

Объяснение:

   У каждого куба 6 граней. Если куб имеет 4 соседа, то свободны от соседей у него две грани.

 Ровно 4 соседа у кубиков, расположенных на ребрах ( без тех, что содержат вершины куба, у которых по 3 соседа).

     Ребер у куба 12, следовательно, на каждом ребре 156:12=13 кубиков с двумя свободными гранями.

      5 соседей у кубиков с одной свободной от соседей гранью. На каждой грани куба таких кубиков 11 рядов по 11 кубиков в каждом, т.е. на одной грани большого куба 11•11=121 (к).

     У куба 6 граней. => На всех гранях куба 6•121=726 кубиков, у которых ровно 5 соседей.

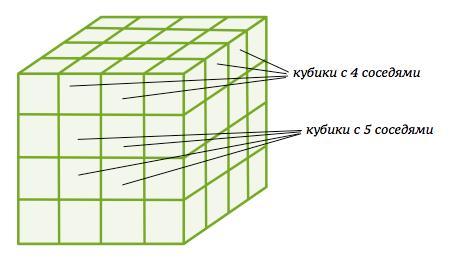
   ***  Картинке в приложенном файле поможет понять расположение кубиков с разным количеством соседних.