Question

N8
В трапеции ABCD (AD: || : BC) биссектрисы углов DAB и ABC
пересеклись на стороне CD. Найдите AB, если AD = 11, BC — 5.
Надо записать Число или дробь

Answer 1

Ответ:

16 ед.

Объяснение:

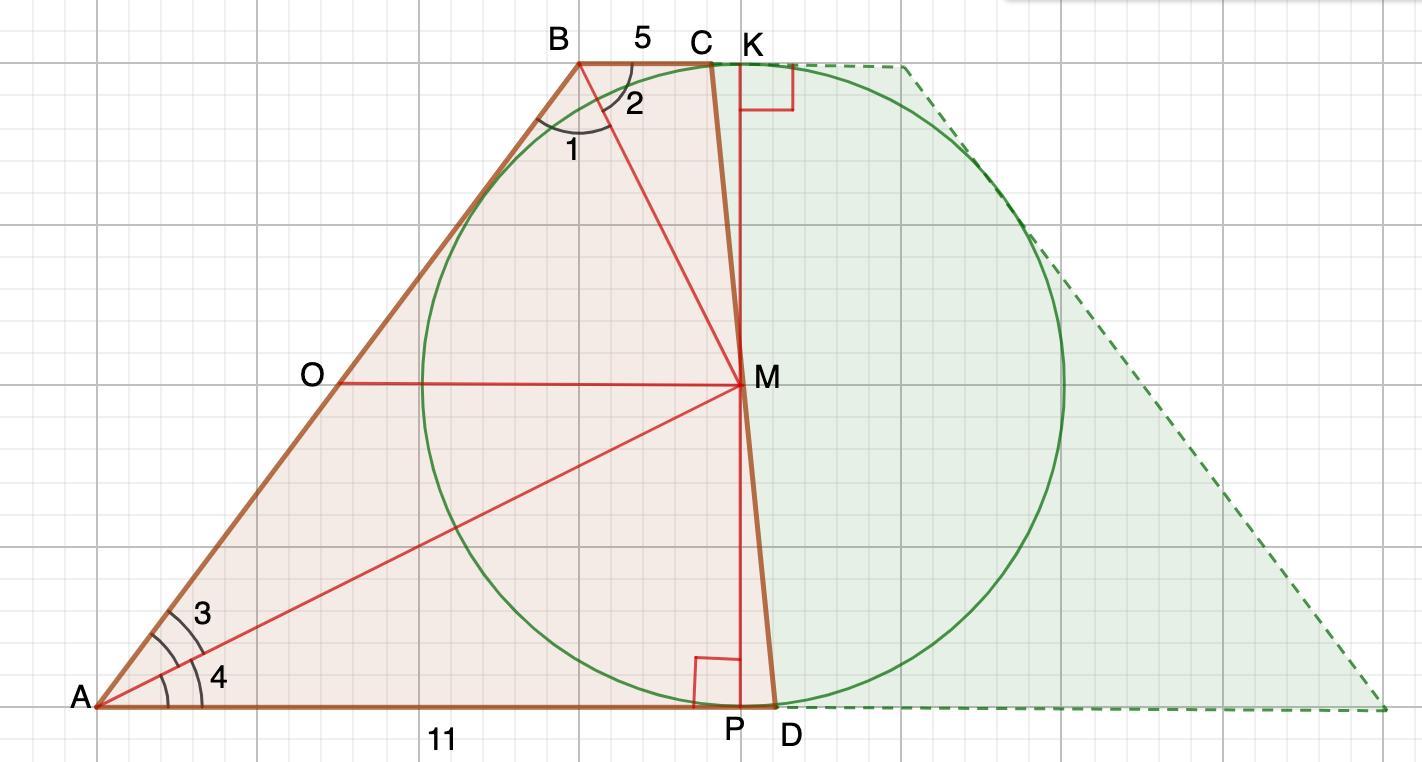
Дано: ABCD - трапеция;

АВ, ВМ - биссектрисы углов DAB и ABC соответственно.

М∈СD

АD=11; ВС=5

Найти: АВ

Решение:

Так как АВ, ВМ - биссектрисы, то точка М будет являться центром окружности, вписанное в эти углы.

Проведем КР ⊥ АD.

• Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.

⇒КР ⊥ ВС.

1. Рассмотрим ΔСКМ и ΔРМD - прямоугольные.

МК=МР=r; ∠СМК=∠РМD - вертикальные.

⇒ ΔСКМ = ΔРМD (по катету и острому углу.

⇒ СМ=МD (как соответственные элементы)

2.  Проведем МО || AD.

СМ=МD (п.1)

• Если отрезок в трапеции проходит через середину одной из его боковых сторон, пересекает вторую боковую сторону и параллелен основанию — этот отрезок можно назвать средней линией этой трапеции.

⇒ МО - средняя линия.

То есть АО=ОВ

• Средняя линия трапеции равна полусумме оснований.

МО=(ВС+AD):2=(5+11):2=8

3. Рассмотрим ΔАВМ.

• Сумма углов трапеции, прилежащих к боковой стороне равна 180°.

⇒∠А+∠В=180°

или

∠3+∠4+∠1+∠2=180°

Так как ∠1=∠2 и ∠3=∠4 (АВ, ВМ - биссектрисы),

то ∠1+∠3=180°:2=90°

⇒ ΔАВМ - прямоугольный.

4. Рассмотрим ΔАВМ - прямоугольный.

АО=ОВ (п.2)

⇒ МО - медиана.

• Медиана, проведенная из вершины прямого угла к гипотенузе равна ее половине.

⇒ АВ = 2ОМ=16