Предмет: Алгебра,
автор: comarad
Сверхсрочно! Завтра сдача!
Задано выражение:
а) Максимально упростите выражение (12 баллов).
б) Найдите значение выражения при n = 25; m = 169
Приложения:
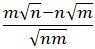
Ответы
Автор ответа:
24
fiiffijc:
МНЕ ПОМОГИТЕ УМОЛЯЮ СРОЧНО
mn−nm=nm(m)2⋅n−(n)2⋅m=nmnm(m−n)==m−nn=25 ; m=169m−n=169−25=132−52=13−5=8
Автор ответа:
19
Ответ:
8
Объяснение:
Для любых действительных чисел a и b таких, что выполняется равенство
.
Для любого неотрицательного числа a справедливо, что
.
a)
б)
n=25; m=169
ок
Похожие вопросы
Предмет: Английский язык,
автор: petuhoffserg91
Предмет: Русский язык,
автор: vershtefi2004
Предмет: Английский язык,
автор: Аноним
Предмет: География,
автор: mironOFF31
Предмет: Математика,
автор: larionovvvv