3 Задачи по геометрии (100 баллов).
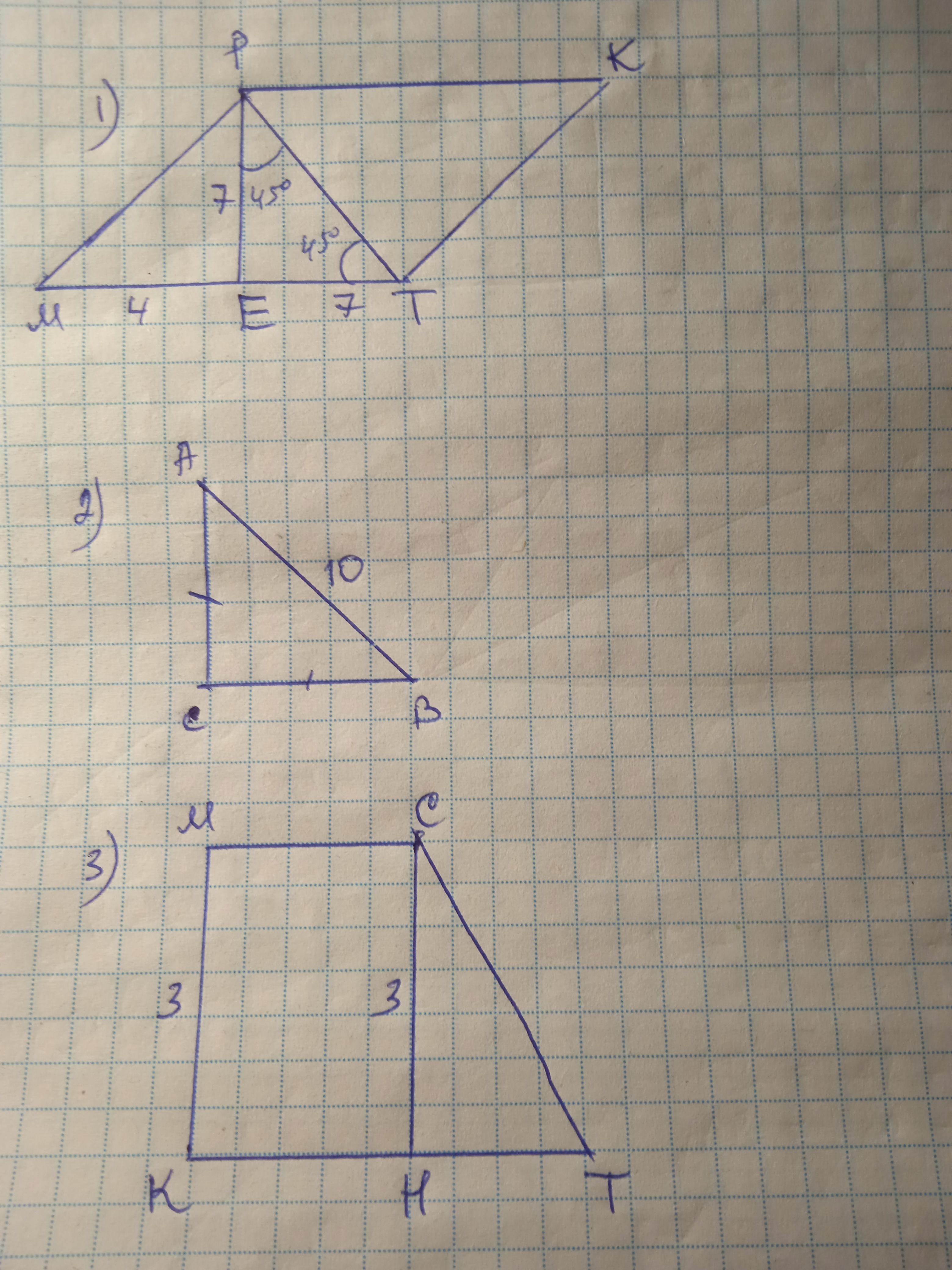
1. В параллелограмме MPKT на стороне MT отмечена точка E, ∠PEM=90°, ∠EPT=45°, ME=4 см, ET=7 см. Найдите площадь параллелограмма.
2. Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой 10 см.
3. В прямоугольной трапеции площадь равна 30 см², периметр 28 см, а меньшая боковая сторона 3 см. Найдите большую боковую сторону.
Ответы
1. Рассмотрим треугольник PET. он прямоуголный (угол PET 90). тогда угол PTE равен 45 (из суммы углов треугольника =180) отсюда следует, что PE=ET=7.
тогда площадь равна S=PE*MT=7*11=77.
3.Площадь прямоугольной трапеции равна произведению полусуммы основания на высоту (в данном случае высота - меньшая боковая сторона, так как трапеция прямоугольная) . Пусть основания равны А и В, тогда А+В / 2 * 3 = 30. Отсюда А + В = 20. Периметр равен 28 см, следовательно, можем найти большую боковую сторону: 28 - (А+В) - 3 = 28 - 20 - 3 = 5 см.
Ответ: 5 см.
2 на фото.

1.
77 см².
ΔЕРТ - прямоугольный, ∠РТЕ=90-45=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°;
ΔРТЕ - равнобедренный, РЕ=ЕТ=7 см
РЕ - высота МРКТ, т.к. РЕ⊥МТ; МТ=4+7=11 см
S(МРКТ)=МТ*РЕ=11*7=77 см²
2.
Пусть АС=ВС=х см. Тогда по теореме Пифагора 10²=2х²
2х²=100; х²=50; х=√50
S=1/2 * AC*BC=1/2 * √50 * √50 = 1/2 * 50 = 25 см²
3.
Дано: КМСТ - трапеция; МК⊥КТ, МК=3 см; S(МКСТ)=30 см², Р(МКСТ)=28 см. Найти СТ.
Проведем высоту СН=МК=3 см;
S(КМСТ)=(СМ+КТ)/2 * СН; 30=(СМ+КТ)/2 * 3;
(СМ+КТ)/2=30/3
СМ+КТ=20 см
СТ=28-20-3=5 см.