Предмет: Алгебра,
автор: Аноним
помогите, пожалуйста!
Вычислить интеграл.
Приложения:
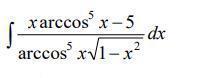
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: слон33
Предмет: Қазақ тiлi,
автор: arunasungatova
Предмет: Английский язык,
автор: tulushenok
Предмет: История,
автор: msudarikova99
Предмет: Алгебра,
автор: 112233msal