Предмет: Геометрия,
автор: livenkoliana1
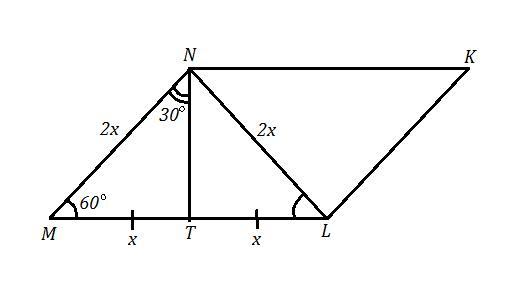
В параллеллограмме MNKL угол равен M равен 60° Высота NT делит сторону ML на дае равные части. Найдите длину диагонали NL если периметр параллеллограмма равен 84 см
Ответы
Автор ответа:
2
Ответ:
MNKL - параллелограмм , NT⊥ML , ∠M=60° ,
ΔMNK: ∠MNT=90°-60°=30°
Против угла в 30° лежит катет, равный половине гипотенузы , значит.
MT=1/2*MN ⇒ MN=2MT .
Если обозначить МТ=х , то MN=2x .
ΔMNL: NT - высота , MT=NL по условию ⇒ высота в треугольнике является одновременно и медианой ⇒ ΔMNL - равнобедренный (MN=NL) и ∠NLM=∠NML=60° . Но тогда и ∠MNL=180°-60°-60°=60° ⇒ ΔMNL - равносторонний .
Значит, NL=ML=MN=2x .
P=MN+NK+KL+ML=84 cм , MN=ML=KL=NK ⇒
MN=ML=KL=NK=84:4=21 cм
Так как NL=MN , то NL=21 см .
Приложения:
Misha55356:
Помогите пожалуйста с заданием по геометрии 11 класс ник Mishka1239 последние задание
Похожие вопросы
Предмет: Русский язык,
автор: Dany20081
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: sahalord1
Предмет: Русский язык,
автор: stevenget04
Предмет: Экономика,
автор: cergei1982