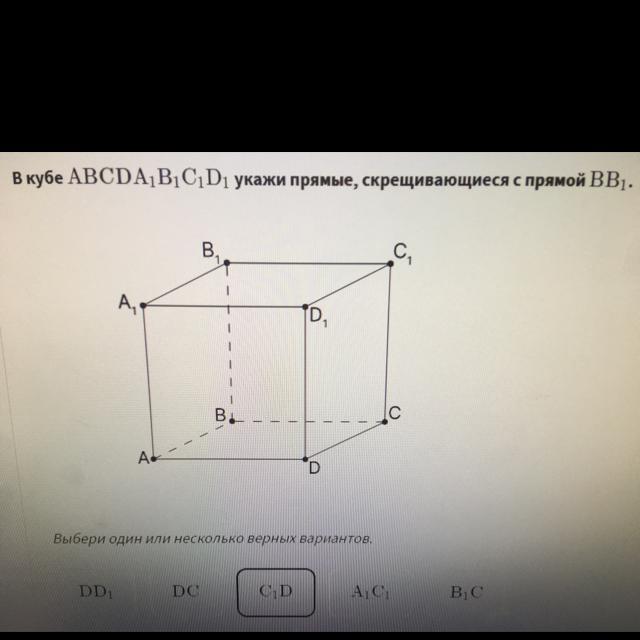
В кубе АBCDA1B1C1D1 укажи прямые скрещивающиеся с прямой BB1
Ответы
Объяснение:
1) 2) и ; и ; и ; расстояние от до - ; - расстояние между и ; - расстояние между и .
Объяснение:
Скрещивающиеся прямые - прямые, не лежащие в одной плоскости.
1) Начинаем с конца условия:
Так как это куб, значит каждые его противоположные грани параллельны.
Прямая лежит в плоскости .
Плоскость - противоположная плоскости , значит
Итак, мы нашли плоскость, параллельную плоскости, в которой лежит прямая
Теперь ищем скрещивающиеся прямые в плоскости с прямой :
По определению, прямые не должны лежать в одной плоскости.
Значит прямые и не подходят, так как прямая находится в плоскости с прямой и находится в плоскости с прямой .
А вот прямые и подходят, так как они не лежат в одной плоскости с прямой
2) Начинаем с начала:
Прямые и не могут быть скрещивающимися, так как лежат в плоскости .
А вот и - скрещивающиеся, так не лежат в одной плоскости.
Также и , и - скрещивающиеся.
Расстояние между скрещивающимися прямыми - отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Найдём расстояние между и :
- точка пересечения диагоналей и
- точка пересечения диагоналей и
, по свойству диагоналей квадрата.
Если прямая перпендикулярна к плоскости, то она перпендикулярна к прямым, лежащим в этой плоскости.
и - расстояние между и .
Найдём также расстояние между и :
, по свойству диагоналей квадрата.
и - расстояние между и .
- прямоугольник, значит , как диагонали прямоугольника, тогда
- прямоугольник, значит
Значит расстояние от до -