Question

В прямоугольном треугольнике ABC с прямым углом А,
к – середина ВС. Через точку к проведены прямые NK и КМ,
параллельные катетам треугольника.
1) Определите вид четырехугольника ANKM, объясните свой
выбор.
2) Найти периметр этого четырехугольника, если катеты
треугольника 12 и 5.

Answer 1

Ответ:

17 ед.

Объяснение:

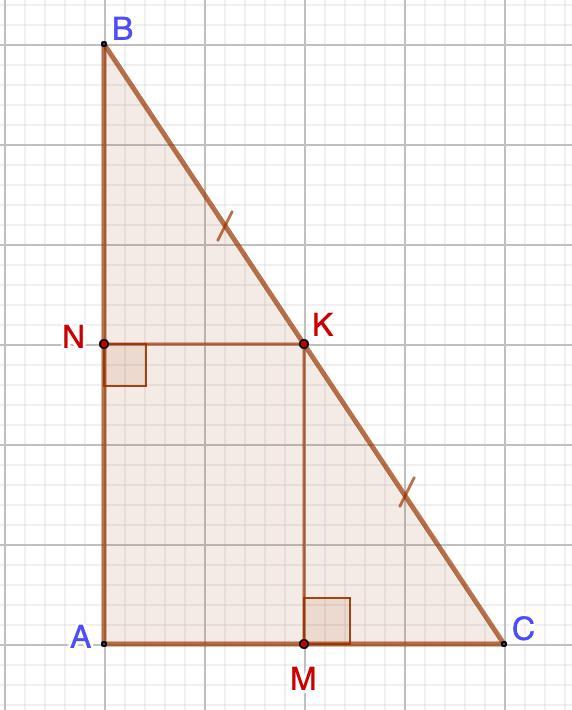
Дано: ΔАВС - прямоугольный.

ВК=КС; NK || AC; КМ || AB.

AB = 12; AC = 5.

Определить: вид ANKM;

Найти: Р (ANKM)

Решение:

1) Рассмотрим ANKM.

NK || AC; КМ || AB (по условию)

⇒ ANKM - параллелограмм (по определению)

• Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.

NK || AC; АС⊥АВ ⇒ NK ⊥ АВ

КМ || AB; АВ ⊥АС ⇒КМ ⊥ АС

Параллелограмм с прямыми углами - прямоугольник.

⇒ ANKM  - прямоугольник.

2) Найдем периметр ANKM.

• Периметр прямоугольника равен удвоенной сумме смежных сторон.

Найдем стороны ANKM.

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — это средняя линия этого треугольника.

• Средняя линия равна половине длины основания.

NK || AC; ВК=КС ⇒ NK- средняя линия;

NK = AC : 2 = 5:2 = 2,5

КМ || AB; ВК=КС ⇒ MK- средняя линия;

MK = AB : 2 = 12:2 = 6

⇒ P (ANKM) = 2· (MK+NK) = 2·(2,5+6)=17 (ед)