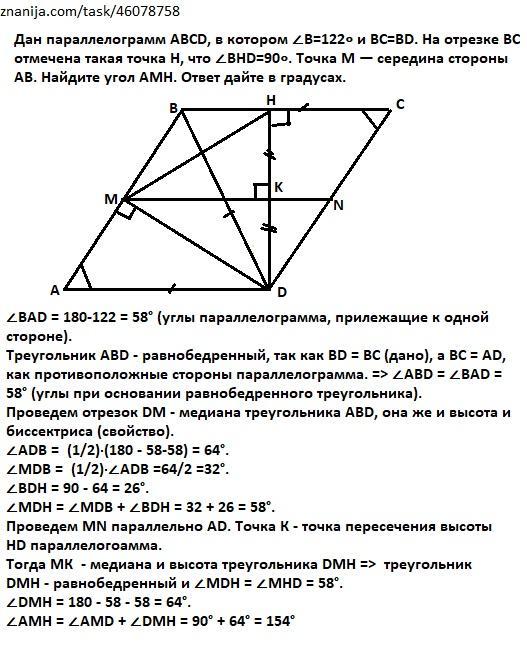
Дан параллелограмм ABCD, в котором ∠B=122∘ и BC=BD. На отрезке BC отмечена такая точка H, что ∠BHD=90∘. Точка M — середина стороны AB. Найдите угол AMH. Ответ дайте в градусах.
Ответы
Ответ:
∠АМН = 154°.
Пошаговое объяснение:
∠BAD = 180-122 = 58° (углы параллелограмма, прилежащие к одной стороне).
Треугольник АВD - равнобедренный, так как BD = ВС (дано), а ВС = AD, как противоположные стороны параллелограмма. => ∠ABD = ∠BAD = 58° (углы при основании равнобедренного треугольника).
Проведем отрезок DM - медиана треугольника ABD, она же и высота и биссектриса (свойство).
∠ADB = (1/2)·(180 - 58-58) = 64°.
∠MDВ = (1/2)·∠ADB =64/2 =32°.
∠ВDН = 90 - 64 = 26°.
∠МDН = ∠MDB + ∠ВDН = 32 + 26 = 58°.
Проведем MN параллельно AD. MN - cредняя линия параллелограмма - отрезок, соединяющий середины двух противолежащих сторон параллелограмма. Точка К - точка пересечения высоты HD параллелограмма и его средней линии. => DK = HK.
Тогда MК - медиана и высота треугольника DMH => треугольник DMH - равнобедренный и ∠МDН = ∠МНD = 58°.
DМН = 180 - 58 - 58 = 64°.
∠АМН = ∠АМD + ∠DМН = 90° + 64° = 154°.