Предмет: Алгебра,
автор: Аноним
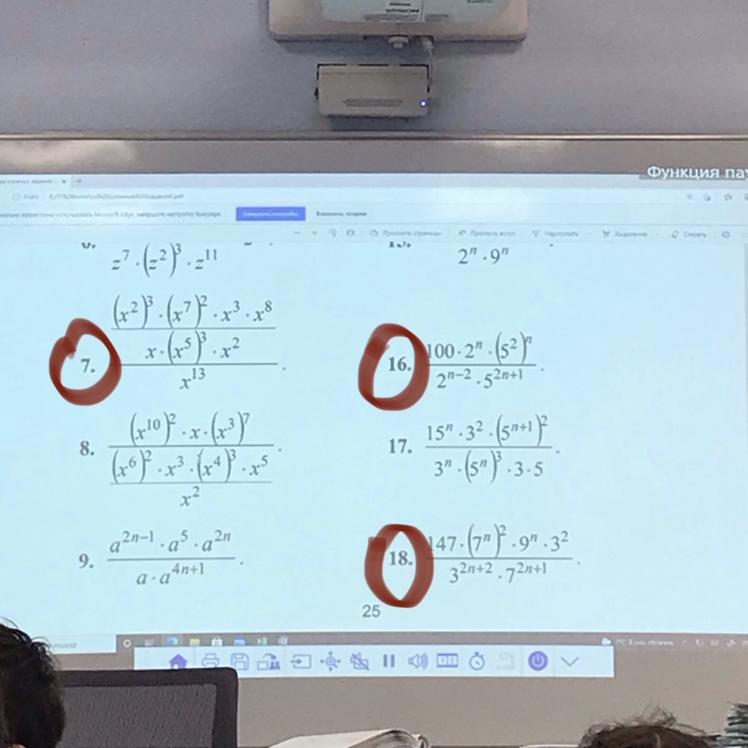
Помогите номера 7 , 16, 18.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Приложения:

NNNLLL54:
а сейчас?
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Убийца56
Предмет: Русский язык,
автор: VeronikaMint
Предмет: Русский язык,
автор: витек2007мищенко
Предмет: Физика,
автор: nastyasiya1
Предмет: Английский язык,
автор: Larisagh