Предмет: Геометрия, автор: ebf17831278

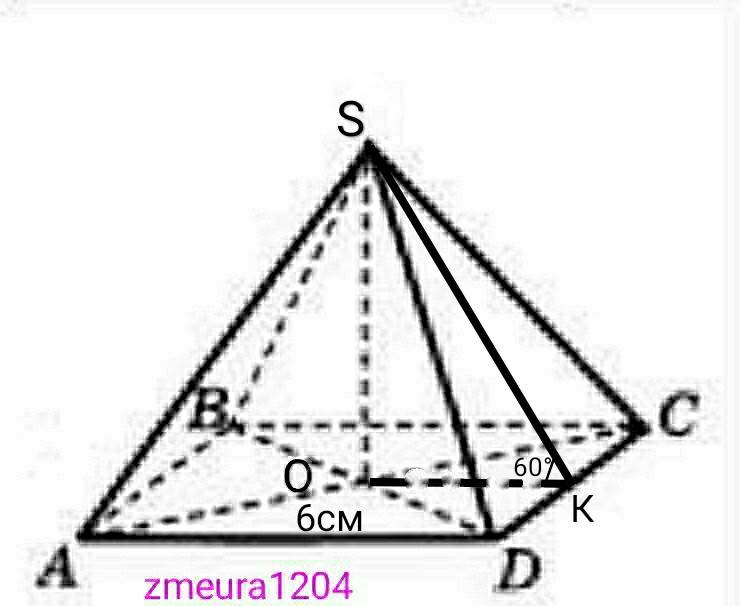
В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 60°. а) Найдите высоту пирамиды б) Найдите площадь полной поверхности пирамиды.

Аноним: Диагональ квадрата 6√2. Проекция ребра на плоскость будет 6√2/2=3√2. tg60=h/3√2. h=3√6. Проекция апофемы 6/2=3. Теорема Пифагора апоф=√(h²+3²)=√(54+9)=3√7. Sбок=1/2*Росн*апоф=9√7. Sосн=6²=36. Sпол=36+9√7

ebf17831278: так у меня пирамида

Аноним: Так я и решала пирамиду.

Аноним: А я ребро наклонила 60°, да это не правильно.

Аноним: Тогда проекция апофемы 6:2=3. tg60=h/3; h=3√3. Теорема Пифагора апоф=√(3²+(3√3)²)=√(9+27)=6. Sбок=1/2*Росн*апоф=1/2*6*4*6=72. Sосн=6²=36. Sпол=72+36=

ebf17831278: Найдите площадь полной поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота – 10. помоги это пожалуйста

Аноним: Sосн=6*а²√3/4=6*6²√3/4=54√3. Sбок=Росн*Н=6*6*10=360. Sпол=2*Sосн+Sбок=360+2*54√3=360+108√3

ebf17831278: спасибо , лучшая

Ответы

Автор ответа: Аноним

Ответ:

Высота пирамиды в равна 3√3см

Sпол=108см²

Объяснение:

ОК=АD/2=6/2=3см

tg<SKO=SO/OK

tg60°=√3

√3=SO/3

SO=3√3 см высота пирамиды.

∆SOK- прямоугольный треугольник

По теореме Пифагора

SK=√(SO²+OK²)=√((3√3)²+3²)=√(27+9)=

=√36=6см

Sбок=1/2*4*АD*SK=2*6*6=72см²

Sосн=АD²=6²=36см²

Sпол=Sбок+Sосн=72+36=108см²

Приложения:

ebf17831278: Найдите площадь полной поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота – 10. помоги это решить пожалуйста

ebf17831278: Помоги алгебру сделать пожалуйста я вопрос добавил

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: адаммии

спиши вставляя пропущенные буквы. Весной жителям (лес) л.. сов плохо приходится. (Крот) кр... ты мышкиполевки, лисы и другие (зверь) зв... рьки страдают от (воды) в.. да.

1 год назад

Предмет: Русский язык, автор: poluchasoi

какие орфограммы в слове такой

1 год назад

Предмет: Русский язык, автор: эмиль61

кто я?поищите в русском языке слова,называют каждого из вас в разных жизненных ситуациях:в семье,в школе, на занятиях спортом.при записи уточняйте написание слов.обсудите,какой частью речи являются эти слова.что еще Вы можете сказать о них?