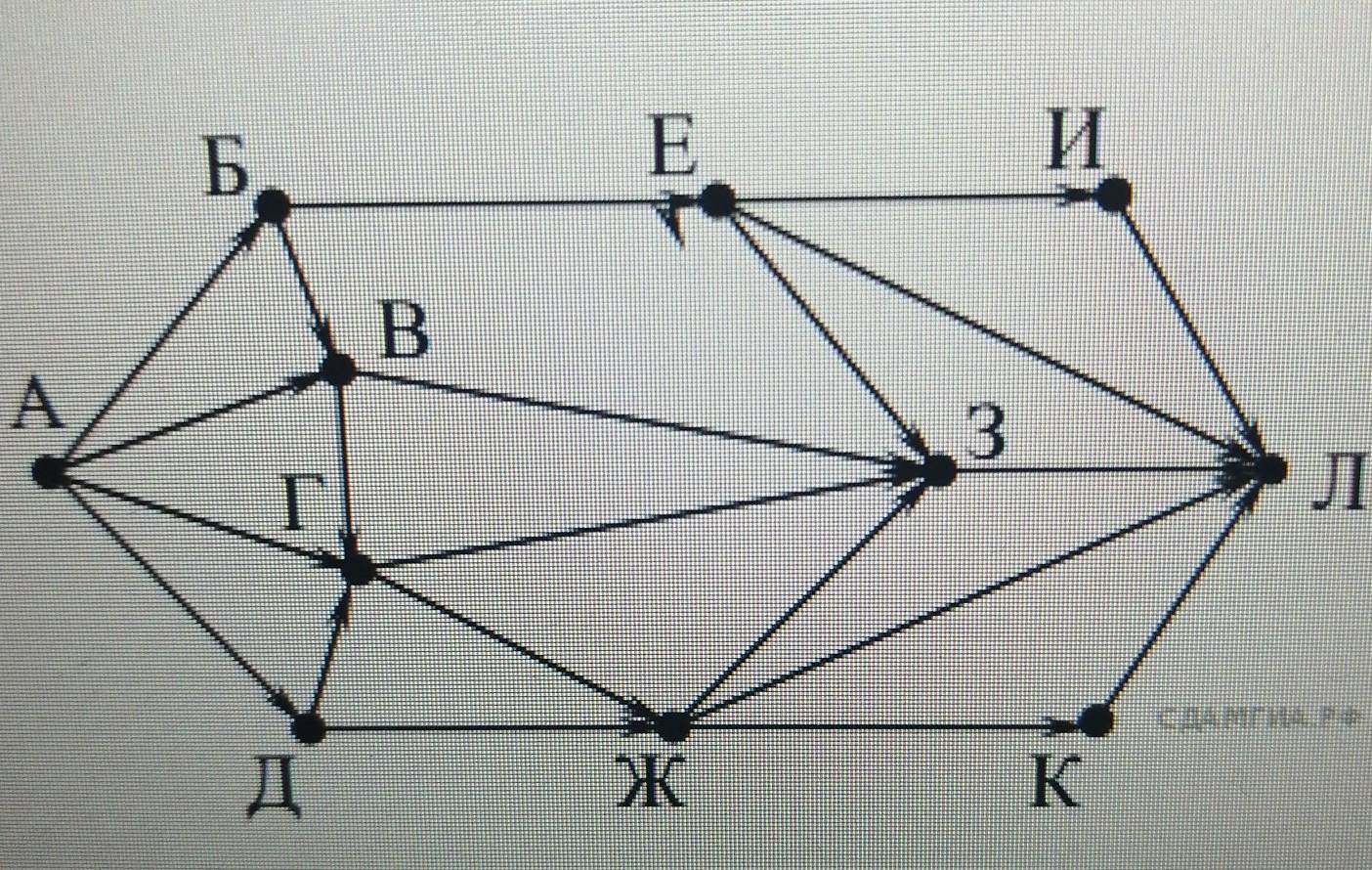
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К и Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через город З?
Ответы
Ответ:
12 различных путей
Объяснение:
Так как в точку Л по условию можно попасть через точку З, то пути к Л от точек И, Е, Ж, К игнорируем. В Л идет один путь из З, далее подсчитываем начиная с конца пути:
З=Е+В+Г+Ж=1+2+4+5=12
Е=Б=1
В=Б+А=1+1=2
Г=В+А+Д=2+1+1=4
Ж=Г+Д=4+1=5
Б=А=1
Д=А=1
Для начала зачеркнем дороги, через которые нельзя попасть из города А в Л через З, это дороги ЕЛ, ЕИ, ИЛ, ЖЛ, ЖК, КЛ.
Далее по порядку к каждому городу ставим в соответствие индекс, который обозначает, сколькими способами можно в этот город попасть. При чем если в город можно попасть из двух городов с индексами 2, то мы складываем эти индексы, а не сами пути, то есть в этот город можно попасть 4 путями. Индекс начального города - 1. Теперь считаем.
Индекс Б - 1, в него ведет дорога из начальной точки.
Индекс В - 2, в него ведут дороги с индексами 1, 1.
Индекс Д - 1, в него ведет дорога из начальной точки.
Индекс Г - 4, в него ведут дороги с индексами 2, 1, 1.
Индекс Е - 1, в него ведет дорога с индексом 1.
Индекс Ж - 5, в него ведут дороги с индексами 4, 1.
Индекс З - 12, в него ведут дороги с индексами 5, 4, 2, 1.
Индекс Л - 12, в него ведет дорога с индексом 12.
Ответ: 12